第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
7. 如图,$OB = BA_{1}=A_{1}A_{2}=A_{2}A_{3}=A_{3}A_{4}=\cdots = A_{2024}A_{2025}=1$,$\angle OBA_{1}=\angle OA_{1}A_{2}=\angle OA_{2}A_{3}=\cdots =\angle OA_{2024}A_{2025}=90^{\circ}$,则线段$OB$,$OA_{1}$,$OA_{2}$,$OA_{3}$,$OA_{4}$,$\cdots$,$OA_{2024}$,$OA_{2025}$中,长度为无理数的线段有
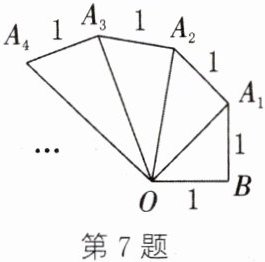
1981
条。
答案:
7.1981
8. 如图,$\triangle ABC$是等腰直角三角形,$\angle BAC = 90^{\circ}$,$\angle EAF = 45^{\circ}$,求证:$BE^{2}+CF^{2}=EF^{2}$。
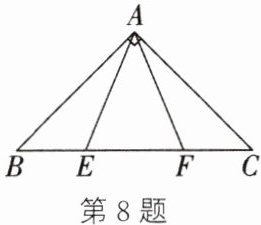

答案:
8.
∵ △ABC是等腰直角三角形,∠BAC = 90°,
∴ ∠ABC = ∠C = 45°。如图,把△ACF绕点A顺时针旋转90°,得到△ABG,连接EG,则∠GAF = 90°,AG = AF,BG = CF,∠ABG = ∠ACF = 45°。
∴ ∠GBE = ∠ABG + ∠ABC = 90°。
∵ ∠GAF = 90°,
∴ ∠GAE = ∠EAF = 45°。在△AEG和△AEF中,
$\begin{cases}$
AG = AF, \\
∠GAE = ∠FAE, \\
AE = AE,
$\end{cases}$
∴ △AEG ≌ △AEF (SAS)。
∴ EF = EG。又
∵ AE = AE,
∵ ∠GBE = 90°,
∴$ BE^{2} + BG^{2} = EG^{2}。$
∴$ BE^{2} + CF^{2} = EF^{2}$

8.
∵ △ABC是等腰直角三角形,∠BAC = 90°,
∴ ∠ABC = ∠C = 45°。如图,把△ACF绕点A顺时针旋转90°,得到△ABG,连接EG,则∠GAF = 90°,AG = AF,BG = CF,∠ABG = ∠ACF = 45°。
∴ ∠GBE = ∠ABG + ∠ABC = 90°。
∵ ∠GAF = 90°,
∴ ∠GAE = ∠EAF = 45°。在△AEG和△AEF中,
$\begin{cases}$
AG = AF, \\
∠GAE = ∠FAE, \\
AE = AE,
$\end{cases}$
∴ △AEG ≌ △AEF (SAS)。
∴ EF = EG。又
∵ AE = AE,
∵ ∠GBE = 90°,
∴$ BE^{2} + BG^{2} = EG^{2}。$
∴$ BE^{2} + CF^{2} = EF^{2}$

9. (新视角·探究题)【问题提出】如图①,在$Rt\triangle ABC$中,AB=AC,D为BC边上一点(不与点B,C重合),以AD为直角边在AD右侧做等腰直角三角形ADE,连接EC。
(1)$\angle ECD$的度数为
(2)线段BC,DC,EC之间有怎样的数量关系?并说明理由。
【类比探究】如图②,若点D在BC边的延长线上,其他条件不变。
(3)试探究线段BD,DC,DE之间满足的数量关系,并说明理由。
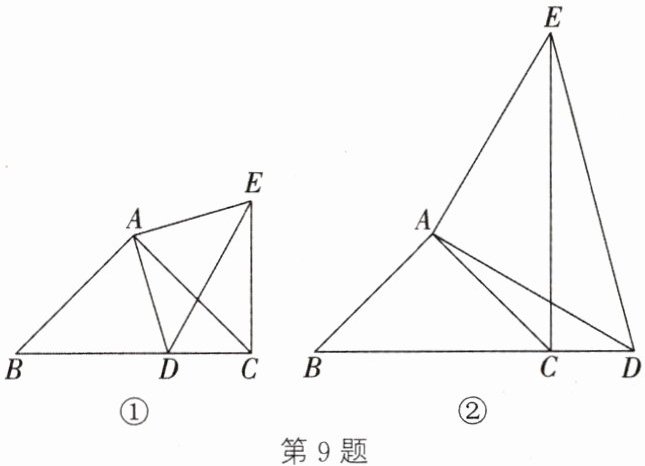
(1)$\angle ECD$的度数为
90°
。(2)线段BC,DC,EC之间有怎样的数量关系?并说明理由。
【类比探究】如图②,若点D在BC边的延长线上,其他条件不变。
(3)试探究线段BD,DC,DE之间满足的数量关系,并说明理由。

答案:
9.
(1)90° 解析:
∵在Rt△ABC中,AB = AC,
∴∠B = ∠ACB = 45°。
∵△ADE是等腰直角三角形,
∴AE = AD,∠DAE = 90° = ∠BAC。
∴∠BAD = ∠CAE = 90° - ∠CAD。
∴△ABD ≌ △ACE。
∴ ∠ACE = ∠B = 45°。
∴∠ECD = ∠ACB + ∠ACE = 90°。
(2)BC = DC + EC 理由:由
(1)知,△ABD ≌ △ACE,
∴CE = BD。
∵BC = DC + BD,
∴BC = DC + EC。$ (3)BD^{2} + CD^{2} = DE^{2} $理由:
∵AB = AC,AE = AD,∠BAD = ∠CAE = 90° + ∠CAD,
∴△ABD ≌ △ACE。
∴∠ACE = ∠B = 45°,CE = BD。
∴∠ECB = ∠ACB + ∠ACE = 90°。
∴∠ECD = 90°。在Rt△ECD中,由勾股定理,得$CE^{2} + CD^{2} = DE^{2},$
∴$BD^{2} + CD^{2} = DE^{2}。$
(1)90° 解析:
∵在Rt△ABC中,AB = AC,
∴∠B = ∠ACB = 45°。
∵△ADE是等腰直角三角形,
∴AE = AD,∠DAE = 90° = ∠BAC。
∴∠BAD = ∠CAE = 90° - ∠CAD。
∴△ABD ≌ △ACE。
∴ ∠ACE = ∠B = 45°。
∴∠ECD = ∠ACB + ∠ACE = 90°。
(2)BC = DC + EC 理由:由
(1)知,△ABD ≌ △ACE,
∴CE = BD。
∵BC = DC + BD,
∴BC = DC + EC。$ (3)BD^{2} + CD^{2} = DE^{2} $理由:
∵AB = AC,AE = AD,∠BAD = ∠CAE = 90° + ∠CAD,
∴△ABD ≌ △ACE。
∴∠ACE = ∠B = 45°,CE = BD。
∴∠ECB = ∠ACB + ∠ACE = 90°。
∴∠ECD = 90°。在Rt△ECD中,由勾股定理,得$CE^{2} + CD^{2} = DE^{2},$
∴$BD^{2} + CD^{2} = DE^{2}。$
查看更多完整答案,请扫码查看


