第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
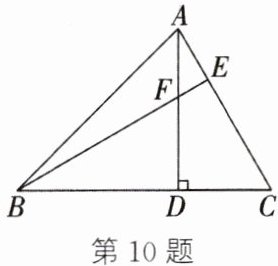
10. (2024·贾汪期中改编)如图,$AD$为$△ABC$的高,$E$为$AC$上一点,$BE$交$AD$于点$F$,且有$BF=AC$,$FD=CD$.
(1)求证:$Rt△BFD≌Rt△ACD$;
(2)求$∠AEB$的度数.
(1)求证:$Rt△BFD≌Rt△ACD$;
(2)求$∠AEB$的度数.

答案:
10.
(1)
∵ AD为△ABC的高,
∴ AD⊥BC.
∴ ∠BDF = ∠ADC = 90°. 在Rt△BFD和Rt△ACD中,$\begin{cases}BF = AC,\\FD = CD,\end{cases}$
∴ Rt△BFD≌Rt△ACD(HL)
(2)
∵ Rt△BFD≌Rt△ACD,
∴ ∠DBF = ∠DAC.
∵ ∠FAE + ∠AEB + ∠EFA = 180°,∠DBF + ∠BDF + ∠BFD = 180°,∠BFD = ∠EFA,
∴ ∠AEB = ∠BDF = 90°
(1)
∵ AD为△ABC的高,
∴ AD⊥BC.
∴ ∠BDF = ∠ADC = 90°. 在Rt△BFD和Rt△ACD中,$\begin{cases}BF = AC,\\FD = CD,\end{cases}$
∴ Rt△BFD≌Rt△ACD(HL)
(2)
∵ Rt△BFD≌Rt△ACD,
∴ ∠DBF = ∠DAC.
∵ ∠FAE + ∠AEB + ∠EFA = 180°,∠DBF + ∠BDF + ∠BFD = 180°,∠BFD = ∠EFA,
∴ ∠AEB = ∠BDF = 90°
11. (新视角·过程性学习)【问题提出】学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】我们不妨将问题用符号语言表示:在$△ABC$和$△DEF$中,$AC=DF$,$BC=EF$,$∠B=∠E$,然后对$∠B$进行分类,可分为“$∠B$是直角、钝角、锐角”三种情况进行探究.
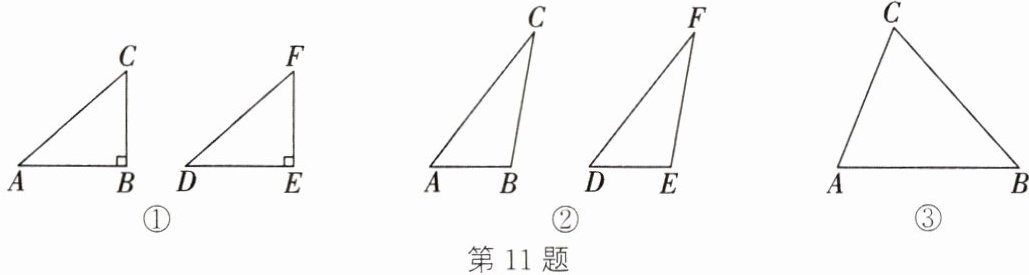
【深入探究】(1)当$∠B$是直角时,如图①,在$△ABC$和$△DEF$中,$AC=DF$,$BC=EF$,$∠B=∠E=90^{\circ }$,根据
(2)当$∠B$是钝角时,如图②,在$△ABC$和$△DEF$中,$AC=DF$,$BC=EF$,$∠B=∠E$,且$∠B$,$∠E$都是钝角,求证:$△ABC≌△DEF$(提示:过点$C$作$CG⊥AB$交$AB$的延长线于点$G$,过点$F$作$FH⊥DE$交$DE$的延长线于点$H$).
(3)当$∠B$是锐角时,在$△ABC$和$△DEF$中,$AC=DF$,$BC=EF$,$∠B=∠E$,且$∠B$,$∠E$都是锐角,请你利用图③,在图③中用尺规作出$△DEF$,使$△DEF$和$△ABC$不全等.
【得出结论】(4)通过以上对“两个三角形满足两边和其中一边的对角对应相等”的情形的研究,你能得出什么结论?
【初步思考】我们不妨将问题用符号语言表示:在$△ABC$和$△DEF$中,$AC=DF$,$BC=EF$,$∠B=∠E$,然后对$∠B$进行分类,可分为“$∠B$是直角、钝角、锐角”三种情况进行探究.
【深入探究】(1)当$∠B$是直角时,如图①,在$△ABC$和$△DEF$中,$AC=DF$,$BC=EF$,$∠B=∠E=90^{\circ }$,根据
HL
,可以知道$Rt△ABC≌Rt△DEF$.(2)当$∠B$是钝角时,如图②,在$△ABC$和$△DEF$中,$AC=DF$,$BC=EF$,$∠B=∠E$,且$∠B$,$∠E$都是钝角,求证:$△ABC≌△DEF$(提示:过点$C$作$CG⊥AB$交$AB$的延长线于点$G$,过点$F$作$FH⊥DE$交$DE$的延长线于点$H$).
(3)当$∠B$是锐角时,在$△ABC$和$△DEF$中,$AC=DF$,$BC=EF$,$∠B=∠E$,且$∠B$,$∠E$都是锐角,请你利用图③,在图③中用尺规作出$△DEF$,使$△DEF$和$△ABC$不全等.
【得出结论】(4)通过以上对“两个三角形满足两边和其中一边的对角对应相等”的情形的研究,你能得出什么结论?

答案:
11.
(1)HL
(2)如图①,过点C作CG⊥AB交AB的延长线于点G,过点F作FH⊥DE交DE的延长线于点H.
∵ ∠ABC = ∠DEF,
∴ 180° - ∠ABC = 180° - ∠DEF,即∠CBG = ∠FEH. 在△CBG和△FEH中,$\begin{cases}∠CBG = ∠FEH,\\∠G = ∠H,\\BC = EF,\end{cases}$
∴ △CBG ≌ △FEH (AAS).
∴ CG = FH. 在Rt△ACG和Rt△DFH中,$\begin{cases}AC = DF,\\CG = FH,\end{cases}$
∴ Rt△ACG ≌ Rt△DFH (HL).
∴ ∠A = ∠D. 在△ABC和△DEF中,$\begin{cases}∠A = ∠D,\\∠ABC = ∠DEF,\\AC = DF,\end{cases}$
∴ △ABC ≌ △DEF(AAS)
(3)如图②,在△ABC和△DEF中,AC = DF,BC = EF,∠B = ∠E,满足了题目中的条件,但很明显,它们不全等
(4)两个三角形满足两边和其中一边的对角对应相等,当这个角是直角或者钝角时,这两个三角形全等;当这个角是锐角时,这两个三角形不一定全等
11.
(1)HL
(2)如图①,过点C作CG⊥AB交AB的延长线于点G,过点F作FH⊥DE交DE的延长线于点H.
∵ ∠ABC = ∠DEF,
∴ 180° - ∠ABC = 180° - ∠DEF,即∠CBG = ∠FEH. 在△CBG和△FEH中,$\begin{cases}∠CBG = ∠FEH,\\∠G = ∠H,\\BC = EF,\end{cases}$
∴ △CBG ≌ △FEH (AAS).
∴ CG = FH. 在Rt△ACG和Rt△DFH中,$\begin{cases}AC = DF,\\CG = FH,\end{cases}$
∴ Rt△ACG ≌ Rt△DFH (HL).
∴ ∠A = ∠D. 在△ABC和△DEF中,$\begin{cases}∠A = ∠D,\\∠ABC = ∠DEF,\\AC = DF,\end{cases}$
∴ △ABC ≌ △DEF(AAS)
(3)如图②,在△ABC和△DEF中,AC = DF,BC = EF,∠B = ∠E,满足了题目中的条件,但很明显,它们不全等
(4)两个三角形满足两边和其中一边的对角对应相等,当这个角是直角或者钝角时,这两个三角形全等;当这个角是锐角时,这两个三角形不一定全等

查看更多完整答案,请扫码查看


