《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

10. 若$\sqrt{8 - x}$为整数，$x$为正整数，则$x$的值为4或7或8。

答案： 10.4或7或8

11. 求下列各式的值：
（1）$\sqrt{9}+\sqrt{\frac{1}{64}}$；
（2）$\sqrt{5^2 - 4^2}$；
（3）$\sqrt{(-3)×(-27)}$；
（4）$\sqrt{1 - \frac{9}{25}}$。

答案： 11.
(1)3$\frac{1}{8}$　
(2)3　
(3)9　
(4)$\frac{4}{5}$

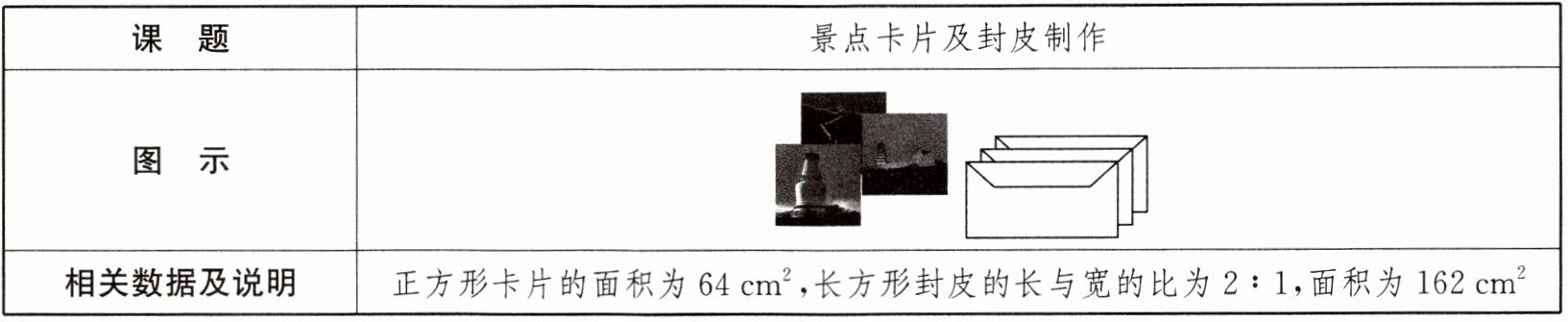
12. （新视角·项目式学习）为宣传某地旅游资源，一中学课外活动小组制作了精美的景点卡片，并为每一张卡片制作了一个特色封皮。A小组成员制作正方形卡片，B小组成员制作长方形封皮。请你通过计算，判断正方形卡片能否直接全部装进长方形封皮中。

答案： 12.设长方形封皮的宽为x(x＞0)cm，则长为2x cm.依题意，得x·2x = 162.整理，得x² = 81，易得x = 9.
∵正方形卡片的面积为64cm²，
∴正方形卡片的边长为$\sqrt{64}$ = 8(cm).
∵9＞8，
∴正方形卡片能直接全部装进长方形封皮中

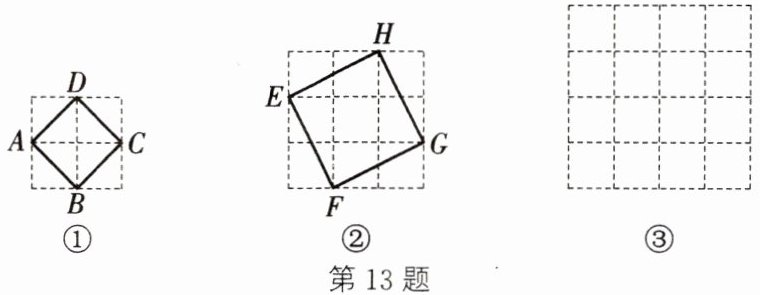
13. (新视角·操作实践题)【阅读理解】在数学学习中，我们常常借助由边长为1的小正方形组成的网格来解决问题，并把由格点(小正方形的顶点)组成的正方形称为格点正方形。图①是由4个边长为1的小正方形组成的网格，容易发现格点正方形$ABCD$的面积为2，则这个格点正方形的边长为$\sqrt{2}$。
【问题解决】
(1)图②是由9个边长为1的小正方形组成的网格，那么格点正方形$EFGH$的边$EH=$$\sqrt{5}$；
(2)在由16个边长为1的小正方形组成的图③中，画出边长为$\sqrt{8}$的格点正方形$MKJI$。

答案：
13.
(1)$\sqrt{5}$　
(2)如图所示