第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
8. (2025· 西安期中)如图,在△ABC 中,AB < AC,AD 平分∠BAC,过点 B 作 BD ⊥ AD 于点 D. 若∠C = 50°,∠CBD = 15°,则∠ABD 的度数为
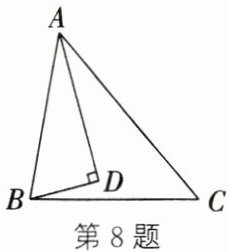
65°
.
答案:
8. 65°
9. (2025· 上海期中)如图,在△ABC 中,D 是边 AB 的中点,E 是边 AC 上一点,过点 B 作 BF // AC,交 ED 的延长线于点 F. 如果 AC = 12,BF = 9,那么 CE 的长为
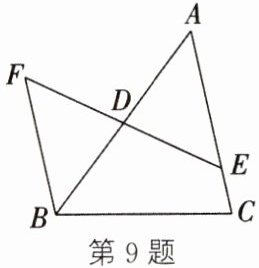
3
.
答案:
9. 3
10. 如图,AD 是△ABC 的中线,E,F 分别是 AD 和 AD 延长线上的点,且 CE // BF. △ECD 与△FBD 全等吗? 请说明理由.


答案:
10. △ECD ≌ △FBD 理由:
∵ AD 是△ABC 的中线,
∴ CD = BD.
∵ CE // BF,
∴ ∠DCE = ∠DBF. 在△ECD 和$\begin{cases} ∠DCE = ∠DBF, \\ CD = BD, \\ ∠EDC = ∠FDB, \end{cases}$
∴ △ECD ≌ △FBD(ASA).
∵ AD 是△ABC 的中线,
∴ CD = BD.
∵ CE // BF,
∴ ∠DCE = ∠DBF. 在△ECD 和$\begin{cases} ∠DCE = ∠DBF, \\ CD = BD, \\ ∠EDC = ∠FDB, \end{cases}$
∴ △ECD ≌ △FBD(ASA).
11. 已知△ABC,求作△DEF,使得△DEF ≌ △ABC.
(1) 如图,根据作图痕迹补全作法;
① 作∠MDN = ∠
③ 以
(2) 这种作一个三角形与已知三角形全等的方法的依据是
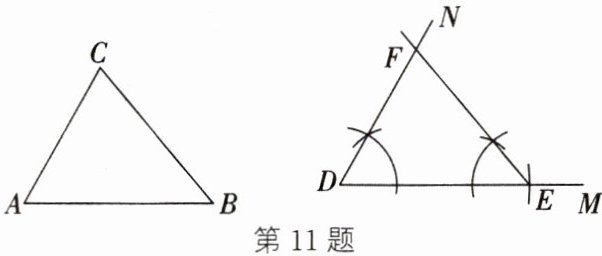
(1) 如图,根据作图痕迹补全作法;
① 作∠MDN = ∠
A
; ② 在射线DM
上截取DE
= AB;③ 以
E
为顶点,以ED
为一边,作∠DEF = ∠B
,EF
交射线 DN 于点 F,则△DEF 即为所求作的三角形.(2) 这种作一个三角形与已知三角形全等的方法的依据是
ASA
.
答案:
11.
(1) ① A ② DM DE ③ E ED B EF
(2) ASA
(1) ① A ② DM DE ③ E ED B EF
(2) ASA
12. (新情境· 日常生活)如图,小明和小华住在同一个小区不同单元楼,他们想要测量小明家所在单元楼 AB 的高度. 首先他们在两栋单元楼之间选定一点 E,然后在点 E 正上方 1 m 处取一点 F 并连接 EF,过点 F 作 FG ⊥ AB 于 G,并测得∠1 + ∠2 = ∠1 + ∠3 = 90°. 已知 BG = EF = 1 m,四边形 BGFE 为长方形,BE = CD = 20 m,BD = 58 m,点 B,E,D 在同一条直线上,求单元楼 AB 的高度.
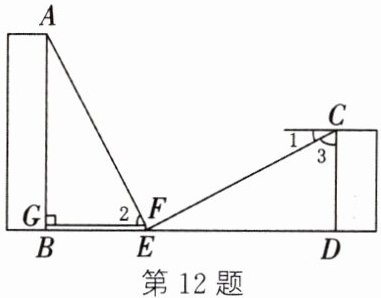

答案:
12.
∵ ∠1 + ∠2 = ∠1 + ∠3 = 90°,
∴ ∠2 = ∠3. 由题意,得 FG ⊥ AB,CD ⊥ BD,FG = BE,
∴ ∠AGF = ∠EDC = 90°.
∵ BE = CD,FG = BE,
∴ FG = CD. 在△AFG 和$\begin{cases} ∠AGF = ∠EDC, \\ FG = CD, \\ ∠2 = ∠3, \end{cases}$
∴ △AFG ≌ △ECD (ASA).
∴ AG = ED = BD - BE = 38 m.
∴ AB = AG + BG = 38 + 1 = 39(m).
∴ 单元楼AB的高度为39 m
∵ ∠1 + ∠2 = ∠1 + ∠3 = 90°,
∴ ∠2 = ∠3. 由题意,得 FG ⊥ AB,CD ⊥ BD,FG = BE,
∴ ∠AGF = ∠EDC = 90°.
∵ BE = CD,FG = BE,
∴ FG = CD. 在△AFG 和$\begin{cases} ∠AGF = ∠EDC, \\ FG = CD, \\ ∠2 = ∠3, \end{cases}$
∴ △AFG ≌ △ECD (ASA).
∴ AG = ED = BD - BE = 38 m.
∴ AB = AG + BG = 38 + 1 = 39(m).
∴ 单元楼AB的高度为39 m
查看更多完整答案,请扫码查看


