《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

8. 如图，下列每个三角形中的三个数之间均具有相同的规律，按此规律，最后一个三角形中y与x之间的关系式为$y=x + 2^{x - 2}(x≥2)$.

答案： $8. y=x + 2^{x - 2}(x\geq2)$

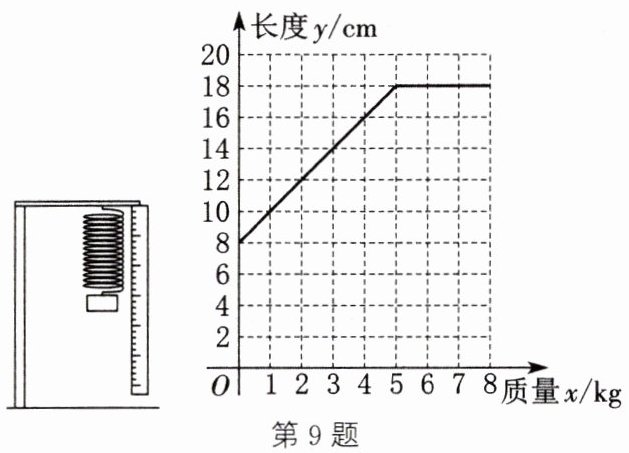
9. 在一次实验中，小明把一根弹簧的上端固定，在其下端悬挂物体，测得弹簧的长度ycm随所挂物体的质量xkg变化关系的图象如图所示：
（1）图中反映哪两个变量之间的关系？
（2）根据图象，补全表格：

（3）弹簧长度是如何随悬挂物体质量的变化而变化的？

答案： 9.
(1)反映了弹簧的长度y cm与所挂物体的质量x kg两个变量之间的关系
(2)根据上图，补全表格：
x/kg 0 1 2 4 5 7
y/cm 8 10 12 16 18 18
(3)由图象得，当所挂物体的质量不超过5kg时，所挂物体的质量每增加1kg，弹簧的长度增加2cm；当所挂物体的质量超过5kg时，弹簧的长度为18cm，不随所挂物体的质量的变化而变化

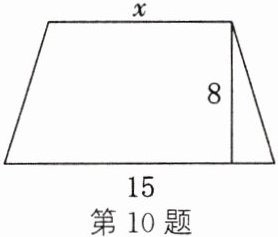
10. (新视角·探究题)如图，梯形的上底长是x，下底长是15，高是8.
（1）写出梯形面积y与上底长x之间的关系式.
（2）填空：

（3）y如何随x的变化而变化？
（4）当 $ x = 0 $ 时，y等于什么？此时它表示的图形是什么？

答案： 10.
(1)梯形面积y与上底长x之间的关系式为y=(x + 15)×8÷2 = 4x + 60
(2)
上底长x … 10 14 18 20 …
梯形面积y … 100 116 132 140 …
(3)当x每增加1时，y增加4
(4)当x = 0时，y = 4×0 + 60 = 60；此时它表示的图形是三角形