《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

9. 如图，在$\triangle ABC$中，$\angle A=90^{\circ}$，利用尺规作图法在$BC$边上求作一点$D$，连接$AD$，使得$AD=\frac{1}{2}BC$（不写作法，保留作图痕迹）。

答案：
9.如图，AD即为所求作
　　　　　　　　

10. 如图，$\triangle ABC$与$\triangle ADE$均为含$30^{\circ}$角的直角三角形，其中$\angle BAC=\angle AED=90^{\circ}$，$\angle B=\angle D=30^{\circ}$，且$E$为$AB$的中点。请仅用无刻度的直尺完成以下作图（保留作图痕迹，不写作法）。
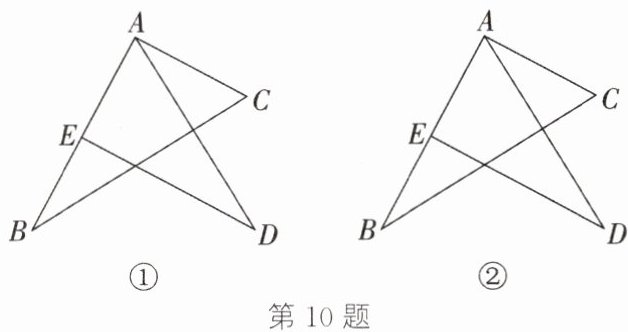
(1) 请你在图①中作出$\triangle ABC$的中线$AM$，并说明这样作的理由；
(2) 请你在图②中作出$\triangle ABC$的中线$BN$。

答案：
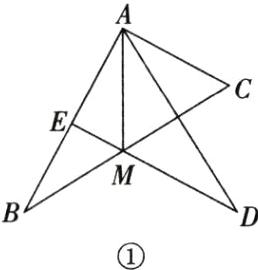
10.
(1)如图①,AM即为所求作　理由:由题意易得DE是AB 的垂直平分线，则AM=BM.
∴∠B=∠BAM=30°.
∴∠CAM=∠BAC−∠BAM=60°.
∵∠C=90°−∠B=60°,
∴△AMC是等边三角形.
∴AM=CM.
∴BM=CM.
∴AM 是△ABC的中线.　　
(2)如图②,BN即为所求作
　　　　　　　　　
　　　　　　　　　

11. 【定义新知】如图①，在$\triangle ABC$中，把$AB$绕点$A$顺时针旋转$\alpha$（$0^{\circ}＜\alpha＜180^{\circ}$）得到$AD$，把$AC$绕点$A$逆时针旋转$\beta$得到$AE$，连接$DE$，当$\alpha+\beta=180^{\circ}$时，我们称$\triangle ADE$是$\triangle ABC$的“旋补三角形”，边$DE$上的中线$AF$叫作$\triangle ABC$的“旋补中线”，点$A$叫作“旋补中心”。
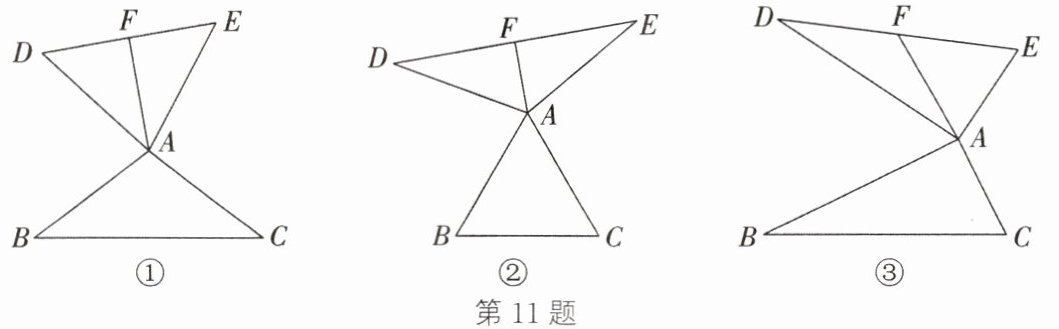
【特例感知】(1) 如图②，$\triangle ADE$是$\triangle ABC$的“旋补三角形”，$AF$是$\triangle ABC$的“旋补中线”，点$A$是“旋补中心”。若$\triangle ABC$为等边三角形，请判断$AF$与$BC$之间的数量关系，并说明理由。
【迁移探究】(2) 如图③，在$\triangle ABC$中，$\angle BAC=90^{\circ}$，$\triangle ADE$是$\triangle ABC$的“旋补三角形”，$AF$是$\triangle ABC$的“旋补中线”，点$A$是“旋补中心”，请你判断(1)中$AF$与$BC$之间的数量关系是否仍然成立，并说明理由。

答案： 11.
(1)BC=2AF　理由:
∵△ABC是等边三角形，
∴AB=AC=BC,∠BAC=60°.
∵△ADE是△ABC的“旋补三角形”,
∴∠BAD+∠CAE=180°,AB=AD,AC=AE.
∴∠DAE=120°,AD=AE=AB=AC=BC.
∴∠D=∠E=30°.
∵F为DE的中点，
∴AF⊥DE,即∠AFD=90°.在△ADF中,∠AFD=90°,∠D=30°,
∴AD=2AF.
∴BC=2AF.　　
(2)
(1)中AF与BC之间的数量关系仍然成立　理由:
∵△ADE是△ABC的“旋补三角形”，
∴∠BAD+∠CAE=180°,AB=AD,AC=AE.
∵∠BAC=90°,
∴∠DAE=90°.
∵AB=AD,∠BAC=∠DAE=90°,AC=AE,
∴△ABC≌△ADE(SAS).
∴BC=DE.
∵在Rt△ADE中,AF为DE边上的中线，
∴DE=2AF.
∴BC=2AF,即
(1)中AF与BC之间的数量关系仍然成立.