第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 在平面直角坐标系中,点 $ P(6,0) $ 位于(
A.$ x $ 轴的正半轴
B.$ x $ 轴的负半轴
C.$ y $ 轴的正半轴
D.$ y $ 轴的负半轴
A
)A.$ x $ 轴的正半轴
B.$ x $ 轴的负半轴
C.$ y $ 轴的正半轴
D.$ y $ 轴的负半轴
答案:
1. A
2. 如果点 $ A(3,m) $ 在 $ x $ 轴上,那么点 $ B(m + 2,m - 3) $ 所在的象限是(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
2. D
3. 已知平面直角坐标系内有一点 $ P(x,x + 2) $,则无论 $ x $ 取何值,点 $ P $ 不可能在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
3. D
4. 已知点 $ P(2m + 4,m - 1) $ 在第一象限,且到 $ x $ 轴的距离为 2,则 $ m = $
3
.
答案:
4. 3
5. 若点 $ P $ 在 $ x $ 轴下方,到 $ x $ 轴的距离是 5,到 $ y $ 轴的距离是 2,则点 $ P $ 的坐标为
(-2,-5)或(2,-5)
.
答案:
5. (-2,-5)或(2,-5)
6. 在平面直角坐标系中,若点 $ P(a,5) $ 到 $ y $ 轴的距离是 2,则 $ a $ 的值是
±2
.
答案:
6. ±2
7. (2024·贾汪段考)如图,点 $ A,B,C $ 都在网格的格点上.若点 $ A $ 的坐标为 $ (0,2) $,点 $ B $ 的坐标为 $ (2,0) $,则点 $ C $ 的坐标为(
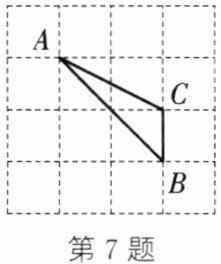
A.$ (2,2) $
B.$ (1,2) $
C.$ (1,1) $
D.$ (2,1) $
D
)
A.$ (2,2) $
B.$ (1,2) $
C.$ (1,1) $
D.$ (2,1) $
答案:
7. D
8. 如图所示为 $ 8×8 $ 的正方形网格.
(1) 在网格中建立平面直角坐标系,以 $ O $ 为坐标原点,使点 $ A $ 的坐标为 $ (-3,5) $,点 $ B $ 的坐标为 $ (-5,3) $;
(2) 若点 $ C $ 的坐标为 $ (-2,0) $,则 $ \triangle ABC $ 是
(3) 在第二象限内的格点上找点 $ P $,使点 $ P $ 与线段 $ AB $ 组成等腰三角形,且腰长是无理数,写出所有符合条件的点 $ P $ 的坐标.
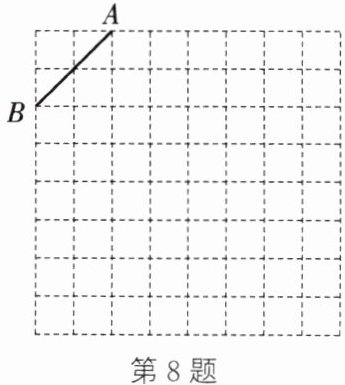
(1) 在网格中建立平面直角坐标系,以 $ O $ 为坐标原点,使点 $ A $ 的坐标为 $ (-3,5) $,点 $ B $ 的坐标为 $ (-5,3) $;
(2) 若点 $ C $ 的坐标为 $ (-2,0) $,则 $ \triangle ABC $ 是
直角
三角形;(3) 在第二象限内的格点上找点 $ P $,使点 $ P $ 与线段 $ AB $ 组成等腰三角形,且腰长是无理数,写出所有符合条件的点 $ P $ 的坐标.

答案:
8.
(1) 如图所示
(2) 直角
(3) 点P的坐标为(-3,1)或(-1,3)或(-2,2)或(-1,1)

8.
(1) 如图所示
(2) 直角
(3) 点P的坐标为(-3,1)或(-1,3)或(-2,2)或(-1,1)

查看更多完整答案,请扫码查看


