第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. (新考向·数学文化)意大利著名画家达·芬奇用如图所示的方法证明了勾股定理.最左边图形中两个正方形的边长分别为$a$,$b$,空白部分的面积为$S_{1}$,最右边图形中空白部分的面积为$S_{2}$.下列等式成立的是(
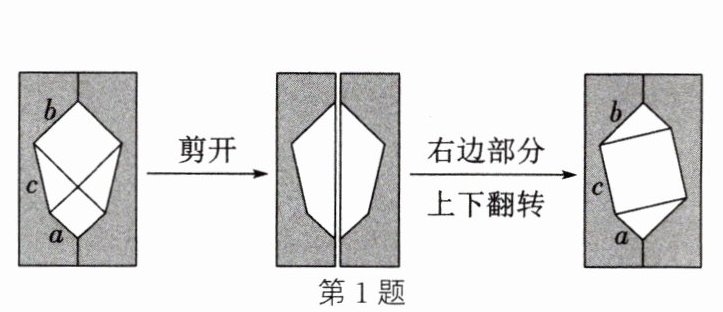
A.$S_{1}=a^{2}+b^{2}+ab$
B.$S_{2}=c^{2}$
C.$S_{2}=c^{2}+\frac{1}{2}ab$
D.$S_{1}=a^{2}+b^{2}+2ab$
A
)
A.$S_{1}=a^{2}+b^{2}+ab$
B.$S_{2}=c^{2}$
C.$S_{2}=c^{2}+\frac{1}{2}ab$
D.$S_{1}=a^{2}+b^{2}+2ab$
答案:
1. A
2. 如图所示为“赵爽弦图”,$\triangle ABH$,$\triangle BCG$,$\triangle CDF$和$\triangle DAE$是四个全等的直角三角形,四边形$ABCD$,$EFGH$都是正方形.如果$AB = 20$,$AH = 12$,那么$FG=$

4
.
答案:
2. 4
3. (新考向·数学文化)我国清代数学家李锐借助三个正方形用出入相补证明了勾股定理.设直角三角形的边长分别是$a$,$b(b > a)$,斜边的长为$c$,作三个边长分别为$a$,$b$,$c$的正方形,把它们拼成如图所示的形状,使$A$,$C$,$E$三点在同一条直线上.若$AB + AC = 10$,四边形$ABHJ$与$\triangle CFK$面积之和为$37$,则正方形$BCIH$的面积为
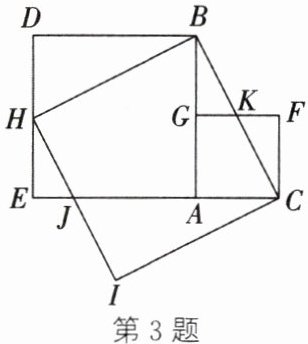
58
.
答案:
3. 58
4. (2023·徐州期中)操作与探究.
(1) 图①是由$20$个边长为$1$的正方形组成的,把它按图①的分割方法分割成五个部分后可拼接成一个大正方形,请你在图②的网格中画出拼接成的大正方形.
(2) 如果(1)中分割成的直角三角形两直角边分别为$a$,$b$,斜边为$c$.请你利用拼成的大正方形证明勾股定理.
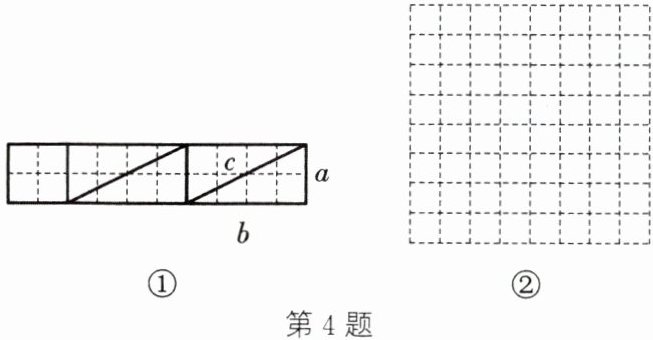
(1) 图①是由$20$个边长为$1$的正方形组成的,把它按图①的分割方法分割成五个部分后可拼接成一个大正方形,请你在图②的网格中画出拼接成的大正方形.
(2) 如果(1)中分割成的直角三角形两直角边分别为$a$,$b$,斜边为$c$.请你利用拼成的大正方形证明勾股定理.

答案:
4.
(1) 如图所示
(2) $\because S_{大正方形} = 4 × \frac{1}{2}ab + (b - a)^2 = 2ab + b^2 - 2ab + a^2 = a^2 + b^2$,且 $S_{大正方形} = c^2$,$\therefore a^2 + b^2 = c^2$

4.
(1) 如图所示
(2) $\because S_{大正方形} = 4 × \frac{1}{2}ab + (b - a)^2 = 2ab + b^2 - 2ab + a^2 = a^2 + b^2$,且 $S_{大正方形} = c^2$,$\therefore a^2 + b^2 = c^2$

查看更多完整答案,请扫码查看


