第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
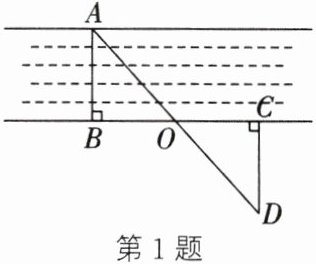
1. 小明利用全等三角形的知识测量河的宽度 $ AB $,设计了如图所示的方案. 在河边选了一点 $ O $,然后在 $ BO $ 的延长线上找一点 $ C $,使 $ OC = OB $,在点 $ C $ 沿与河边垂直的方向直走到点 $ D $,观察到 $ A $,$ O $,$ D $ 三点在同一条直线上. 测得 $ CD $ 的长,就是河的宽度 $ AB $,小明这种设计方案的原理是(
A.$ SSS $
B.$ SAS $
C.$ ASA $
D.$ AAS $
C
)
A.$ SSS $
B.$ SAS $
C.$ ASA $
D.$ AAS $
答案:
1. C
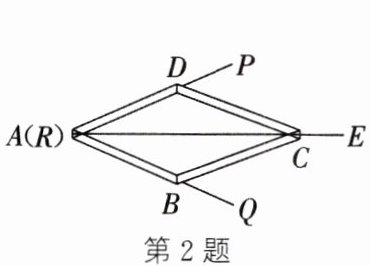
2. 如图,小敏做了一个角平分仪 $ ABCD $,其中 $ AB = AD $,$ BC = DC $,将仪器上的点 $ A $ 与 $ \angle PRQ $ 的顶点 $ R $ 重合,调整 $ AB $ 和 $ AD $,使它们分别落在角的两边上,过点 $ A $,$ C $ 画一条射线 $ AE $,$ AE $ 就是 $ \angle PRQ $ 的平分线. 此角平分仪的画图原理是根据仪器结构,可得 $ \triangle ABC \cong \triangle ADC $,这样就有 $ \angle QAE = \angle PAE $,则说明这两个三角形全等的依据是(
A.$ SAS $
B.$ ASA $
C.$ AAS $
D.$ SSS $
D
)
A.$ SAS $
B.$ ASA $
C.$ AAS $
D.$ SSS $
答案:
2. D
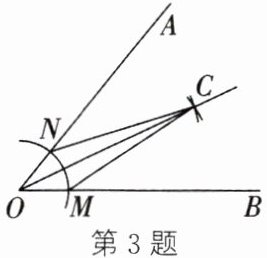
3. (2025·铜山期中)用直尺和圆规作一个角的平分线的示意图如图所示,得 $ \angle AOC = \angle BOC $,则证明这两个角所在的三角形全等的依据是
SSS
.
答案:
3. SSS
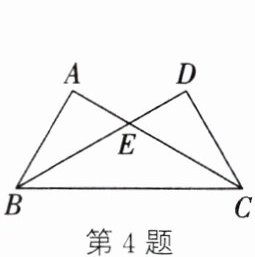
4. (2025·睢宁期中改编)如图,$ \triangle ABC \cong \triangle DCB $,若 $ AC = 6 $,$ DE = 2 $,则 $ BE $ 的长为
4
.
答案:
4. 4
5. 如图,在 $ \triangle ABF $ 和 $ \triangle DCE $ 中,$ AB = CD $,$ AF = DE $,$ BE = CF $,且点 $ B $,$ E $,$ F $,$ C $ 在同一条直线上. $ \angle DEB $ 和 $ \angle AFC $ 相等吗?请说明理由.
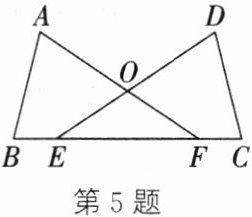

答案:
5. ∠DEB=∠AFC 理由:
∵BE=CF,
∴BE+EF=FC+EF,即 BF=CE。在△ABF 和△DCE 中,
$\begin{cases}AB = CD \\AF = DE \\BF = CE\end{cases}$
∴△ABF≌△DCE(SSS)。
∴∠AFB=∠DEC。
∴∠DEB=∠AFC。
∵BE=CF,
∴BE+EF=FC+EF,即 BF=CE。在△ABF 和△DCE 中,
$\begin{cases}AB = CD \\AF = DE \\BF = CE\end{cases}$
∴△ABF≌△DCE(SSS)。
∴∠AFB=∠DEC。
∴∠DEB=∠AFC。
6. 如图,点 $ E $,$ F $ 在 $ BC $ 上,$ BE = CF $,$ \angle B = \angle C $,添加一个条件,不能判定 $ \triangle ABF \cong \triangle DCE $ 的是(
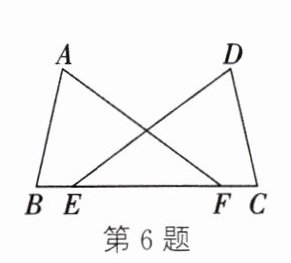
A.$ \angle A = \angle D $
B.$ \angle AFB = \angle DEC $
C.$ AB = DC $
D.$ AF = DE $
D
)
A.$ \angle A = \angle D $
B.$ \angle AFB = \angle DEC $
C.$ AB = DC $
D.$ AF = DE $
答案:
6. D
7. 如图,两棵大树相距 $ 13m $,小华从点 $ B $ 沿 $ BC $ 走向点 $ C $,行走一段时间后到达点 $ E $,此时他仰望两棵大树的顶点 $ A $ 和 $ D $,两条视线的夹角正好为 $ 90^{\circ} $,且 $ EA = ED $. 已知大树 $ AB $ 的高为 $ 5m $,小华行走的速度为 $ 1m/s $,则小华行走的时间是
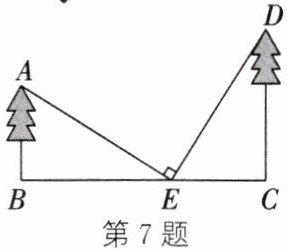
8
$ s $.(小华的身高忽略不计)
答案:
7. 8
查看更多完整答案,请扫码查看


