第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
7. 如图,在$7×7$的正方形网格图中,每个小正方形的边长都为$1$,点$A$,$B$,$C$,$D$,$E$,$F$均在格点上,那么到线段$AB$两个端点距离相等的点的轨迹是(
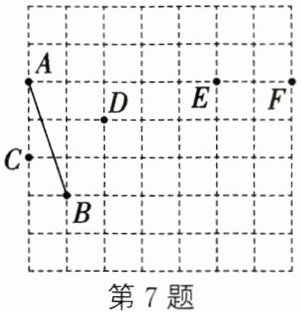
A.直线$CD$
B.直线$CE$
C.直线$DE$
D.直线$DF$
C
)
A.直线$CD$
B.直线$CE$
C.直线$DE$
D.直线$DF$
答案:
7.C
8. 如图,在$\triangle ABC$中,$AB = AC$,$AB$的垂直平分线分别交$AC$,$AB$于点$D$,$E$。若$\triangle ABC$和$\triangle BDC$的周长分别为$40\mathrm{cm}$和$25\mathrm{cm}$,则$BC =$
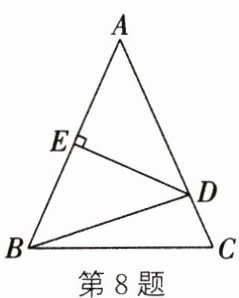
10
$\mathrm{cm}$。
答案:
8.10
9. (2025·徐州期末)如图,在$\triangle ABC$中,$\angle ABC = 60^{\circ}$。
(1)作$\angle ABC$的平分线$BE$,边$BC$的垂直平分线$MN$,$BE$与$MN$相交于点$P$(尺规作图,不写作法,保留作图痕迹);
(2)求$\angle PCB$的度数(写出推理过程)。
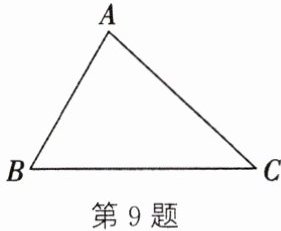
(1)作$\angle ABC$的平分线$BE$,边$BC$的垂直平分线$MN$,$BE$与$MN$相交于点$P$(尺规作图,不写作法,保留作图痕迹);
(2)求$\angle PCB$的度数(写出推理过程)。

答案:
9.
(1)如图,射线BE和直线MN即为所求作
(2)如图,连接PC.
∵BE为∠ABC的平分线,∠ABC=60°,
∴∠PBC= $\frac{1}{2}$∠ABC=30°.
∵直线MN为线段BC的垂直平分线,
∴BP=CP.
∴∠PCB=∠PBC=30°

9.
(1)如图,射线BE和直线MN即为所求作
(2)如图,连接PC.
∵BE为∠ABC的平分线,∠ABC=60°,
∴∠PBC= $\frac{1}{2}$∠ABC=30°.
∵直线MN为线段BC的垂直平分线,
∴BP=CP.
∴∠PCB=∠PBC=30°

10. (新视角·探究题)【问题发现】我们知道“线段垂直平分线上的点到线段两端的距离相等”,那么不在线段垂直平分线上的点到线段两端的距离大小如何判断呢?
【自主研究】
(1)如图①,直线$l$是线段$AB$的垂直平分线,点$P$在直线$l$的左侧,经测量,$PA < PB$,请证明这个结论。
【迁移研究】
(2)如图②,直线$l$是线段$AB$的垂直平分线,点$C$在直线$l$外,且与点$A$在直线$l$的同侧,$D$是直线$l$上的任意一点,连接$AD$,$BC$,$CD$。试判断$BC$和$AD + CD$之间的大小关系,并说明理由。
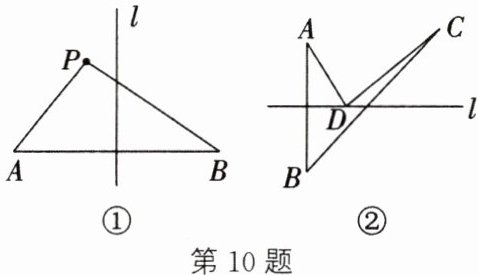
【自主研究】
(1)如图①,直线$l$是线段$AB$的垂直平分线,点$P$在直线$l$的左侧,经测量,$PA < PB$,请证明这个结论。
【迁移研究】
(2)如图②,直线$l$是线段$AB$的垂直平分线,点$C$在直线$l$外,且与点$A$在直线$l$的同侧,$D$是直线$l$上的任意一点,连接$AD$,$BC$,$CD$。试判断$BC$和$AD + CD$之间的大小关系,并说明理由。

答案:
10.
(1)如图①,设PB交直线l于点M,连接AM.
∵直线l是线段AB的垂直平分线,
∴AM=BM.
∴PB=PM+MB=PM+AM.
∵PM+AM>PA,
∴PA<PB
(2)AD+CD≥BC 理由:如图②,当点D不在线段BC 上时,连接BD.
∵直线l是线段AB的垂直平分线,
∴AD=BD.
∵BD+CD>BC,
∴AD+CD>BC;当点D在线段BC 上时,AD+CD=BC.综上可知,AD+CD≥BC

10.
(1)如图①,设PB交直线l于点M,连接AM.
∵直线l是线段AB的垂直平分线,
∴AM=BM.
∴PB=PM+MB=PM+AM.
∵PM+AM>PA,
∴PA<PB
(2)AD+CD≥BC 理由:如图②,当点D不在线段BC 上时,连接BD.
∵直线l是线段AB的垂直平分线,
∴AD=BD.
∵BD+CD>BC,
∴AD+CD>BC;当点D在线段BC 上时,AD+CD=BC.综上可知,AD+CD≥BC

查看更多完整答案,请扫码查看


