《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

10. (2024·丰县期中)如图,$AB = DE$,$AC = DC$,$CE = CB$.求证:$\angle 1 = \angle 2$.

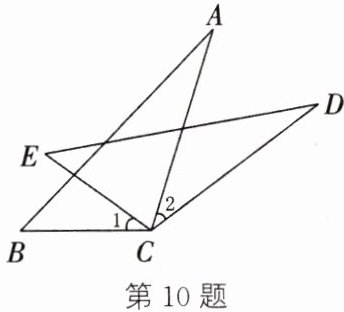
答案： 10. 在△ABC和△DEC中，$\begin{cases}AB = DE,\\AC = DC,\\CB = CE,\end{cases}$
∴ △ABC≌△DEC(SSS).
∴ ∠ACB = ∠DCE.
∴ ∠ACB - ∠ACE = ∠DCE - ∠ACE，即∠1 = ∠2

11. 如图,在$\triangle ABC$中,$AB = AC$,$D$是$BC$的中点,连接$AD$.求证:$AD\perp BC$.

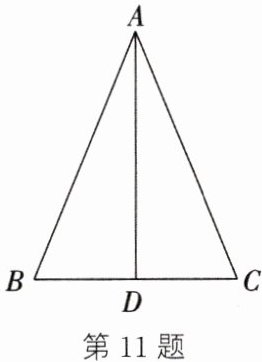
答案： 11.
∵ D是BC的中点，
∴ BD = CD.在△ABD和△ACD中，$\begin{cases}AB = AC,\\AD = AD,\\BD = CD,\end{cases}$
∴ △ABD≌△ACD(SSS).
∴ ∠BDA = ∠CDA.
又
∵ ∠BDA + ∠CDA = 180°，
∴ ∠BDA = ∠CDA = 90°.
∴ AD⊥BC

12. 如图,点$B$,$F$,$C$,$E$在同一条直线上,$FB = CE$,$AB = DE$,$AC = DF$.求证:
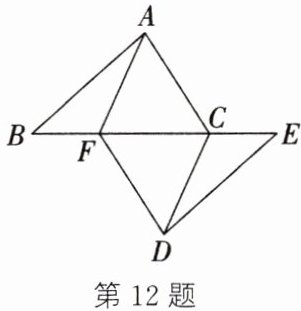
(1)$\triangle ABC\cong\triangle DEF$;
(2)$AF = CD$.

答案： 12.
(1)
∵ FB = CE，
∴ FB + FC = CE + FC，即BC = EF.在
△ABC和△DEF中，$\begin{cases}BC = EF,\\AB = DE,\\AC = DF,\end{cases}$
∴ △ABC≌△DEF(SSS)
(2)
∵ △ABC≌△DEF，
∴ ∠B = ∠E.在△ABF和△DEC中，$\begin{cases}FB = CE,\\∠B = ∠E,\\AB = DE,\end{cases}$
∴ △ABF≌△DEC(SAS).
∴ AF = CD

13. (新考向·传统文化)"风筝飞满天,笑语乐无边",由喜闻乐见的风筝可以抽象得到一种特殊的四边形——筝形.如图,在四边形$ABCD$中,$AB = AD$,$CB = CD$,我们把这种两组邻边分别相等的四边形叫作筝形.
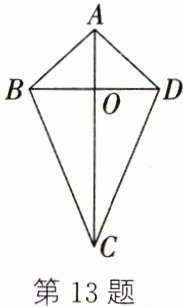
(1)初步认识筝形后,数学活动小组的同学通过观察、测量、折纸等方法猜想筝形有什么性质,请你试着写出图中筝形的两条性质(定义除外):AC⊥BD;△ABC≌△ADC.
(2)选择题(1)中你写出的其中一条筝形的性质进行证明.
(3)若$AC = 10$,$BD = 6$,求筝形$ABCD$的面积.

答案： 13.
(1) 答案不唯一，如AC⊥BD △ABC≌△ADC
(2) 选择不唯一，如△ABC≌△ADC
∵ AB = AD，BC = CD，AC = AC，
∴ △ABC≌△ADC(SSS)
(3) 由
(1)知，AC⊥BD，
∴ $S_{筝形ABCD} = S_{△ABD} + S_{△BCD} = \frac{1}{2}BD \cdot AO + \frac{1}{2}BD \cdot CO = \frac{1}{2}BD \cdot (AO + CO) = \frac{1}{2}BD \cdot AC = \frac{1}{2} × 10 × 6 = 30$