第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 如图,某同学不小心把一块三角形玻璃打碎成三部分,现要去配制一块与原来相同的三角形玻璃,那么应带(
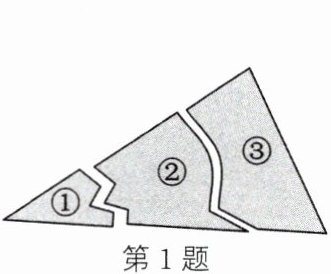
A.①
B.②
C.③
D.无法确定
C
)
A.①
B.②
C.③
D.无法确定
答案:
1. C
2. (2024· 泉山期中)如图,在△ABC 和△ADC 中,∠BAC = ∠DAC. 若添加一个条件就能直接利用“ASA”判定△ABC ≌ △ADC,则可添加的条件是(

A.∠B = ∠D
B.∠BCA = ∠DCA
C.AB = AD
D.BC = DC
B
)
A.∠B = ∠D
B.∠BCA = ∠DCA
C.AB = AD
D.BC = DC
答案:
2. B
3. (2024· 徐州期末)如图,在△ABC 中,AD ⊥ BC,垂足为 D,AD 平分∠BAC,则△ABD ≌ △ACD 的根据是
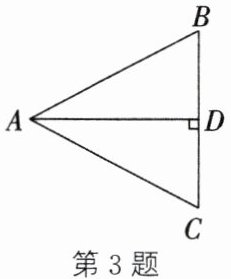
ASA
.
答案:
3. ASA
4. 如图,点 B,E,C,F 在同一条直线上,AB // DE,且 AB = DE. 若直接根据“ASA”判定△ABC ≌ △DEF,则需要添加的一个条件是

∠A = ∠D
.
答案:
4. ∠A = ∠D
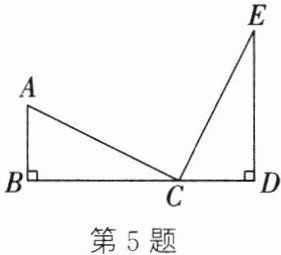
5. 如图,点 C 在线段 BD 上,AB ⊥ BD,ED ⊥ BD,∠ACB = ∠CED,BC = DE.
(1) 求证:△ABC ≌ △CDE;
(2) 若 AB = 2,DE = 4,求 BD 的长.
(1) 求证:△ABC ≌ △CDE;
(2) 若 AB = 2,DE = 4,求 BD 的长.

答案:
5.
(1)
∵ AB ⊥ BD,ED ⊥ BD,
∴ ∠B = ∠D = 90°. 在△ABC 和△CDE中,$\begin{cases} ∠B = ∠D, \\ BC = DE, \\ ∠ACB = ∠CED, \end{cases}$
∴ △ABC ≌ △CDE(ASA)
(2)
∵ △ABC ≌ △CDE,
∴ CD = AB = 2,BC = DE = 4.
∴ BD = BC + CD = 4 + 2 = 6
(1)
∵ AB ⊥ BD,ED ⊥ BD,
∴ ∠B = ∠D = 90°. 在△ABC 和△CDE中,$\begin{cases} ∠B = ∠D, \\ BC = DE, \\ ∠ACB = ∠CED, \end{cases}$
∴ △ABC ≌ △CDE(ASA)
(2)
∵ △ABC ≌ △CDE,
∴ CD = AB = 2,BC = DE = 4.
∴ BD = BC + CD = 4 + 2 = 6
6. 如图,AB = AC,EC 与 BF 交于点 O,∠B = ∠C,∠A = 60°,∠B = 25°,则∠AEC 为(

A.60°
B.95°
C.75°
D.85°
B
)
A.60°
B.95°
C.75°
D.85°
答案:
6. B
7. 如图,在 Rt△ABC 中,∠ACB = 90°,BC = 2 cm,CD ⊥ AB 于点 D,在 AC 上取一点 E,使 EC = BC,过点 E 作 EF ⊥ AC 交 CD 的延长线于点 F. 若 EF = 5 cm,则 AE =

3
cm.
答案:
7. 3
查看更多完整答案,请扫码查看


