《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

5. 图①是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图②是由图①放入长方形内得到的,$\angle BAC = 90^{\circ}$,$AB = 6$,$BC = 10$,点$D$,$E$,$F$,$G$,$H$,$I$都在长方形$KLMJ$的边上,则长方形$KLMJ$的面积为(B)

A.$420$
B.$440$
C.$430$
D.$410$

答案： 5. B

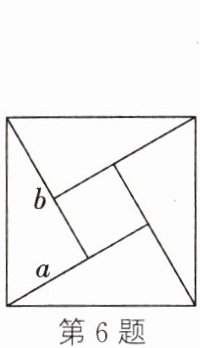
6. 如图所示的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较短直角边长为$a$,较长直角边长为$b$.如果小正方形的面积为$1$,大正方形的面积为$9$,那么$(a - b)^{2}$为1.

答案： 6. 1

7. (2024·丰县段考)如图,点$A$,$B$,$D$在同一条直线上,且$\angle A=\angle D=\angle CBE = 90^{\circ}$,$AB = DE$.
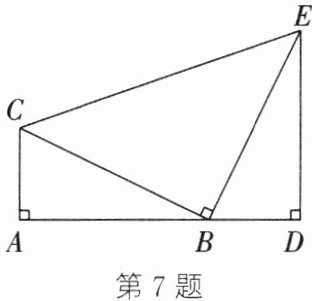
(1) 求证:$\triangle CAB\cong\triangle BDE$;
(2) 若设$BC = c$,$AB = a$,$AC = b$,试利用这个图形验证勾股定理.

答案： 7.
(1) $\because \angle A = 90°$，$\therefore \angle ABC + \angle ACB = 90°$。$\because \angle CBE = 90°$，$\therefore \angle ABC + \angle DBE = 180° - \angle CBE = 90°$。$\therefore \angle ACB = \angle DBE$。 在 $\triangle CAB$ 和 $\triangle BDE$ 中，$\begin{cases} \angle A = \angle D, \\ \angle ACB = \angle DBE, \\ AB = DE, \end{cases}$
$\therefore \triangle CAB \cong \triangle BDE$ (AAS)
(2) $\because \triangle CAB \cong \triangle BDE$，$\therefore AB = DE = a$，$AC = DB = b$，$BC = EB = c$。$\because$ 点 $A$，$B$，$D$ 在同一条直线上，且 $\angle A = \angle D = \angle CBE = 90°$，$\therefore$ 四边形 $ACED$ 是直角梯形。$\therefore S_{四边形ACED} = \frac{1}{2}(AC + DE) \cdot AD = \frac{1}{2}(b + a) \cdot (a + b)$。又 $\because S_{四边形ACED} = 2 × \frac{1}{2}ab + \frac{1}{2}c^2$，$\therefore \frac{1}{2}(b + a)(a + b) = 2 × \frac{1}{2}ab + \frac{1}{2}c^2$，即 $a^2 + b^2 = c^2$

8. (新考向·数学文化)弦图(如图①)在三国时期被赵爽发明,是证明勾股定理几何方法中最为重要的一种图形.2002年国际数学家大会在北京召开,大会的会标是我国古代数学家赵爽画的“弦图”,体现了数学研究中的继承和发展.在学习了勾股定理后,小亮同学受此启发,探究后发现,若将$4$个直角边长为$a$,$b$、斜边长为$c$的直角三角形(图②中涂色部分)拼成如图所示的五边形.通过两种方法计算它的面积可以验证勾股定理,请利用图②完成勾股定理的验证.

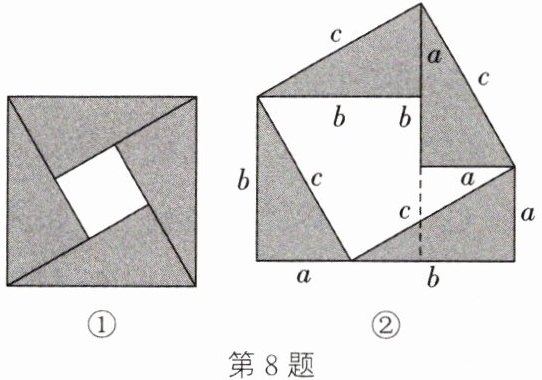
答案：
8. 如图，用数字表示面积的编号 $\because c^2 = S_2 + S_3 + S_4 + S_5$，$b^2 = S_1 + S_2 + S_6$，$a^2 = S_3 + S_7$，$S_1 = S_5 = S_4 = S_6 + S_7$，$\therefore a^2 + b^2 = S_3 + S_7 + S_1 + S_2 + S_6 = S_2 + S_3 + S_1 + (S_6 + S_7) = S_2 + S_3 + S_4 + S_5 = c^2$，$\therefore a^2 + b^2 = c^2$