《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

9. 如图，在网格中，每个小正方形的边长均为$1$，点$A$，$B$，$C$，$P$都在格点(网格线的交点)上，且点$P$在$\triangle ABC$的边$AC$上，则$\angle PAB+\angle PBA$的度数是$45^{\circ}$.

答案： 9. $45^{\circ}$

10. 如图，$AD = 8$，$CD = 6$，$\angle ADC = 90^{\circ}$，$AB = 26$，$BC = 24$，则该图形的面积为96.

答案： 10. 96

11. (新情境·日常生活)如图，某小区在规划建设时，准备在住宅楼和临街的拐角处规划一块绿化用地（四边形$ABCD$）.已知$AB = 12\mathrm{m}$，$BC = 9\mathrm{m}$，$CD = 8\mathrm{m}$，$AD = 17\mathrm{m}$，技术人员通过测量确定了$\angle ABC = 90^{\circ}$.
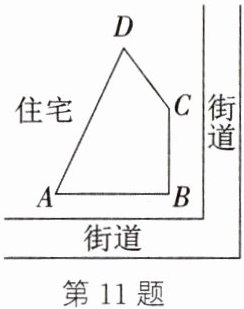
(1) 为了方便居民出入，技术人员计划在绿化用地中开辟一条从点$A$到点$C$的小路，请问这条小路的最短长度是多少米？
(2) 这块绿化用地的面积是多少平方米？

答案：
11.
(1)如图，连接AC.
∵$\angle ABC = 90^{\circ}$，$AB = 12m$，$BC = 9m$，
∴$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{12^{2}+9^{2}}=15(m)$.
∴这条小路的最短长度是15m
(2)
∵$CD = 8m$，$AD = 17m$，$AC = 15m$，
∴$AC^{2}+CD^{2}=15^{2}+8^{2}=17^{2}=AD^{2}$.
∴$\angle ACD = 90^{\circ}$.
∴$S_{四边形ABCD}=S_{\triangle ABC}+S_{\triangle ACD}=\frac{1}{2}AB\cdot BC+\frac{1}{2}AC\cdot CD=\frac{1}{2}×12×9+\frac{1}{2}×15×8=54 + 60 = 114(m^{2})$.
∴这块绿化用地的面积是$114m^{2}$

12. (新视角·探究题)定义：如图，点$M$，$N$把线段$AB$分割成$AM$，$MN$，$NB$.若以$AM$，$MN$，$NB$为边的三角形是一个直角三角形，则称$M$，$N$是线段$AB$的“勾股分割点”.
(1) 已知点$M$，$N$把线段$AB$分割成$AM$，$MN$，$NB$.若$AM = 2$，$MN = 3$，$NB = 4$，则$M$，$N$是线段$AB$的“勾股分割点”吗？请说明理由.
(2) 已知$M$，$N$是线段$AB$的“勾股分割点”.
① “善思小组”提出问题：若$MN$为以$AM$，$MN$，$NB$为边的三角形的最长边，且$AM = BN = 1$，求$AB$的长；
② “智慧小组”提出问题：若$AM$为以$AM$，$MN$，$NB$为边的三角形的直角边，且$AM = 4$，$AB = 12$，请直接写出$BN$的长.

答案： 12.
(1)不是 理由：
∵$AM^{2}+MN^{2}=2^{2}+3^{2}=13\neq NB^{2}$，
∴以AM，MN，NB为边的三角形不是一个直角三角形.
∴M，N不是线段AB的“勾股分割点”.
(2)①
∵M，N是线段AB的“勾股分割点”，MN为以AM，MN，NB为边的三角形的最长边，且$AM = BN = 1$，
∴$MN^{2}=AM^{2}+NB^{2}=2$.
∴$MN=\sqrt{2}$(负值不符合题意，舍去).
∴AB的长为$AM + BN + MN=\sqrt{2}+2$ ②3或5