《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

1. 在$\triangle ABC$中，已知$\angle B=\angle C$，则(B)

A.$AB=BC$
B.$AB=AC$
C.$BC=AC$
D.$\angle A=60^{\circ}$

答案： 1. B

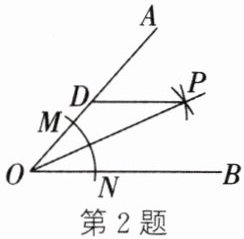
2. (易错题)如图，在$\angle AOB$中，以点$O$为圆心，以适当长度为半径画弧，分别交$OA$，$OB$于点$M$，$N$，再分别以点$M$，$N$为圆心，大于$\frac{1}{2}MN$的长为半径画弧，两弧交于点$P$，连接$OP$，过点$P$作$PD// OB$交$OA$于点$D$。若$OD=3$，则$PD$的长为3。

答案： 2. 3　易错分析:易将角平分线的作图与垂直平分线的作图混淆，平行线的性质掌握不明.

3. 如图，$D$为$\triangle ABC$内一点，$CD$平分$\angle ACB$，$BE\perp CD$，垂足为$D$，交$AC$于点$E$。若$\angle A=\angle ABE$，$BD=1$，$BC=3$，则$AC$的长为5。

答案： 3. 5

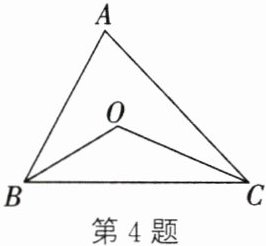
4. 如图，在$\triangle ABC$中，$\angle ABC$和$\angle ACB$的平分线交于点$O$。
(1) 尺规作图：过点$O$作$BC$的平行线$MN$，分别交$AB$，$AC$于点$M$，$N$（不写作法，保留作图痕迹）；
(2) 在(1)的条件下，求证：$MN=BM+CN$。

答案：
4.
(1) 如图，MN即为所求作
(2) $\because$ $\angle ABC$和$\angle ACB$的平分线交于点O，$\therefore$ $\angle MBO=\angle OBC$，$\angle OCN=\angle OCB$. $\because$ $MN// BC$，$\therefore$ $\angle OBC = \angle MOB$，$\angle NOC = \angle OCB$. $\therefore$ $\angle MBO=\angle MOB$，$\angle NOC=\angle OCN$. $\therefore$ $BM=MO$，$ON=CN$. $\therefore$ $MN=MO+ON=BM+CN$

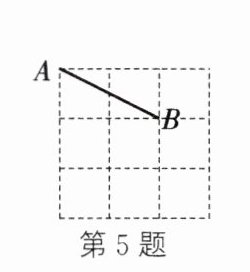
5. 在如图所示的正方形网格图中，点$A$，$B$均在格点(小正方形的顶点)上，连接$AB$，以$AB$为一边，在格点上找一点$C$，使得$\triangle ABC$为等腰三角形的点$C$有(D)

A.1个
B.2个
C.3个
D.4个

答案： 5. D

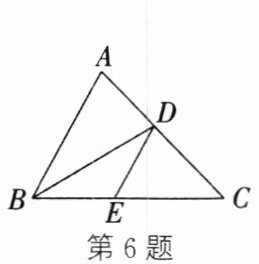
6. 如图，$BD$是$\triangle ABC$的角平分线，过点$D$作$DE// AB$交$BC$于点$E$。若$CE=4$，$DE=3$，则$BC$的长为(C)

A.5
B.6
C.7
D.8

答案： 6. C

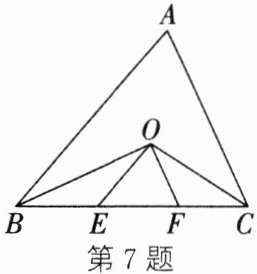
7. 如图，在$\triangle ABC$中，角平分线$BO$和$CO$相交于点$O$，$OE// AB$，$OF// AC$，$BC=2a$，则$\triangle OEF$的周长为2a。

答案： 7. 2a