第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
10. 如图,在平面直角坐标系中,四边形ABCD是正方形,点A的坐标为(1,0),点B的坐标为(-2,4),点D在第一象限,则点C的坐标为
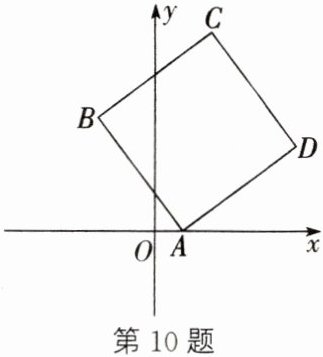
(2,7)
.
答案:
10. (2,7)
11. 如图,在平面直角坐标系中,A(a,0),B(b,0),其中a,b满足|a+1|+(b-3)²=0.
(1) 填空:a=
(2) 如果在第三象限内有一点M(-2,m),请用含m的式子表示△ABM的面积;
(3) 在(2)的条件下,当m=-2时,在y轴上有一点P,使得△ABP的面积与△ABM的面积相等,请求出点P的坐标.
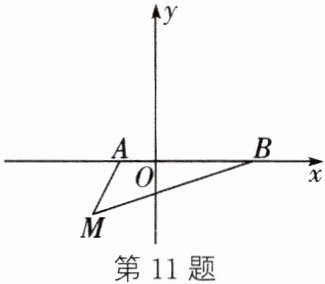
(1) 填空:a=
-1
,b=3
;(2) 如果在第三象限内有一点M(-2,m),请用含m的式子表示△ABM的面积;
(3) 在(2)的条件下,当m=-2时,在y轴上有一点P,使得△ABP的面积与△ABM的面积相等,请求出点P的坐标.

答案:
11.
(1) - 1 3
(2)由
(1)得A(- 1,0),B(3,0),
∴AB = 4.
∴S△ABM = $\frac{1}{2}$AB·(- m) = $\frac{1}{2}$×4×(- m) = - 2m
(3)当m = - 2时,S△ABM = - 2×(- 2) = 4.
∴S△ABP = $\frac{1}{2}$AB·|y_P| = 2|y_P|.
∴2|y_P| = 4.
∴y_P = ±2.
∴点P的坐标为(0,2)或(0, - 2)
(1) - 1 3
(2)由
(1)得A(- 1,0),B(3,0),
∴AB = 4.
∴S△ABM = $\frac{1}{2}$AB·(- m) = $\frac{1}{2}$×4×(- m) = - 2m
(3)当m = - 2时,S△ABM = - 2×(- 2) = 4.
∴S△ABP = $\frac{1}{2}$AB·|y_P| = 2|y_P|.
∴2|y_P| = 4.
∴y_P = ±2.
∴点P的坐标为(0,2)或(0, - 2)
12. (数形结合思想)如图,在平面直角坐标系中,O是坐标原点,过点A(8,6)分别作x轴和y轴的平行线,交y轴于点B,交x轴于点C,M是线段AB的中点,点P从点M出发沿M-A-C向终点C运动,速度为每秒2个单位长度.设点P运动的时间为t秒.
(1) 请直接写出点B和点C的坐标:B(
(2) 用含有t的代数式表示线段AP的长度;
(3) 作线段OP,OM,当△MOP的面积等于直角梯形AMOC面积的$\frac{1}{3}$时,求t的值,并求出此时点P的坐标.
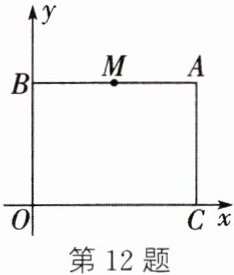
(1) 请直接写出点B和点C的坐标:B(
0
,6
),C(8
,0
);(2) 用含有t的代数式表示线段AP的长度;
(3) 作线段OP,OM,当△MOP的面积等于直角梯形AMOC面积的$\frac{1}{3}$时,求t的值,并求出此时点P的坐标.

答案:
12.
(1)0 6 8 0
(2)
∵M是线段AB的中点,
∴AM = $\frac{1}{2}$AB = 4.当点P运动到点A时,所需时间为4÷2 = 2(秒),当点P运动到点C时,所需时间为(4 + 6)÷2 = 5(秒),
∴当0≤t≤2时,AP = AM - PM = 4 - 2t;当2<t≤5时,AP = 2t - 4. 综上所述,AP = $\begin{cases}4 - 2t(0\leq t\leq 2),\\2t - 4(2<t\leq 5)\end{cases}$
(3)
∵直角梯形AMOC的面积 = $\frac{1}{2}$(AM + OC)·AC = $\frac{1}{2}$×(4 + 8)×6 = 36,
∴S△MOP = $\frac{1}{3}$×36 = 12.当0≤t≤2时,如图①,S△MOP = $\frac{1}{2}$MP·OB = $\frac{1}{2}$·2t·6 = 12,解得t = 2.
∴MP = 4,此时点P与点A重合.
∴P(8,6).当2<t≤5时,如图②,S△AMP + S△POC = S梯形OCAM - S△POM = $\frac{2}{3}$S梯形OCAM = 24,由
(2)知,AP = 2t - 4,则CP = AC - AP = 6 - (2t - 4) = 10 - 2t,
∴$\frac{1}{2}$AP·AM + $\frac{1}{2}$CP·OC = $\frac{1}{2}$(2t - 4)·4 + $\frac{1}{2}$(10 - 2t)·8 = 24,解得t = 2(舍去).
∴t = 2,P(8,6)

12.
(1)0 6 8 0
(2)
∵M是线段AB的中点,
∴AM = $\frac{1}{2}$AB = 4.当点P运动到点A时,所需时间为4÷2 = 2(秒),当点P运动到点C时,所需时间为(4 + 6)÷2 = 5(秒),
∴当0≤t≤2时,AP = AM - PM = 4 - 2t;当2<t≤5时,AP = 2t - 4. 综上所述,AP = $\begin{cases}4 - 2t(0\leq t\leq 2),\\2t - 4(2<t\leq 5)\end{cases}$
(3)
∵直角梯形AMOC的面积 = $\frac{1}{2}$(AM + OC)·AC = $\frac{1}{2}$×(4 + 8)×6 = 36,
∴S△MOP = $\frac{1}{3}$×36 = 12.当0≤t≤2时,如图①,S△MOP = $\frac{1}{2}$MP·OB = $\frac{1}{2}$·2t·6 = 12,解得t = 2.
∴MP = 4,此时点P与点A重合.
∴P(8,6).当2<t≤5时,如图②,S△AMP + S△POC = S梯形OCAM - S△POM = $\frac{2}{3}$S梯形OCAM = 24,由
(2)知,AP = 2t - 4,则CP = AC - AP = 6 - (2t - 4) = 10 - 2t,
∴$\frac{1}{2}$AP·AM + $\frac{1}{2}$CP·OC = $\frac{1}{2}$(2t - 4)·4 + $\frac{1}{2}$(10 - 2t)·8 = 24,解得t = 2(舍去).
∴t = 2,P(8,6)

查看更多完整答案,请扫码查看


