第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 如图,若直接用“AAS”来判定$\triangle ACD\cong\triangle ABE$,则需要添加的条件是(
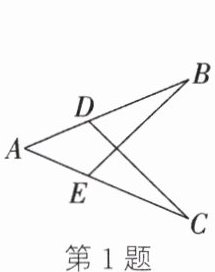
A.$\angle AEB=\angle ADC,BE=CD$
B.$AC=AB,\angle B=\angle C$
C.$AC=AB,AD=AE$
D.$\angle AEB=\angle ADC,\angle B=\angle C$
A
)
A.$\angle AEB=\angle ADC,BE=CD$
B.$AC=AB,\angle B=\angle C$
C.$AC=AB,AD=AE$
D.$\angle AEB=\angle ADC,\angle B=\angle C$
答案:
1. A
2. 在$\triangle ABC$中,$\angle A=60^{\circ},\angle B=50^{\circ},BC=8$,下列条件能判定$\triangle ABC\cong\triangle DEF$的是(
A.$\angle D=60^{\circ},\angle E=50^{\circ},DF=8$
B.$\angle D=60^{\circ},\angle F=50^{\circ},EF=8$
C.$\angle E=50^{\circ},\angle F=70^{\circ},EF=8$
D.$\angle D=60^{\circ},\angle F=70^{\circ},DE=8$
C
)A.$\angle D=60^{\circ},\angle E=50^{\circ},DF=8$
B.$\angle D=60^{\circ},\angle F=50^{\circ},EF=8$
C.$\angle E=50^{\circ},\angle F=70^{\circ},EF=8$
D.$\angle D=60^{\circ},\angle F=70^{\circ},DE=8$
答案:
2. C
3. (新视角·操作实践题)如图,$AM$是一段斜坡,$AB$是水平线. 欢欢为了测量斜坡上一点$C$的竖直高度$CN$,他在点$C$处立上一根竹竿$CF$,竹竿$CF$与斜坡$AM$垂直,在点$D$处垂下一根绳子$DE$,与斜坡$AM$的交点是$E$,绳子$DE$可以在竹竿$CF$上自由滑动. 当$DE=AC$时,测得$CE=2m$,则$CN=$
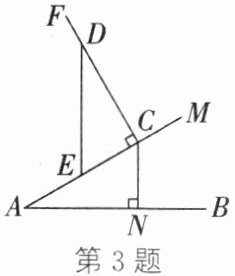
2
m. 其中,运用到的判定三角形全等的依据是AAS
.
答案:
3. 2 AAS
4. 如图,$\angle BAD=\angle CAD$,若要直接利用“AAS”判定$\triangle ABD\cong\triangle ACD$,则需要添加的一个条件是

∠B=∠C
.
答案:
4. ∠B=∠C
5. 如图,点$B,F,C,E$在同一条直线上,$\angle A=\angle D,AB // DE,BF=EC$. 求证:$AC=DF$.
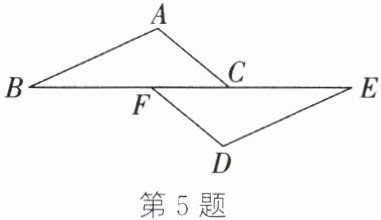

答案:
5.
∵ BF=EC,
∴ BF+FC=EC+FC, 即 BC=EF.
∵ AB//DE,
∴ ∠B=∠E. 在 △ABC 和 △DEF 中,
$\begin{cases}\angle A = \angle D, \\\angle B = \angle E, \\BC = EF,\end{cases}$
∴ △ABC≌△DEF(AAS).
∴ AC=DF
∵ BF=EC,
∴ BF+FC=EC+FC, 即 BC=EF.
∵ AB//DE,
∴ ∠B=∠E. 在 △ABC 和 △DEF 中,
$\begin{cases}\angle A = \angle D, \\\angle B = \angle E, \\BC = EF,\end{cases}$
∴ △ABC≌△DEF(AAS).
∴ AC=DF
6. (2023·铜山期中改编)如图,在$\triangle ABC$中,$D,E$分别是边$AB,AC$上的点,过点$C$作平行于$AB$的直线,交$DE$的延长线于点$F$. 若$DE=FE,AB=7,CF=4$,则$BD$的长为(
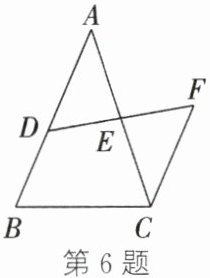
A.3.5
B.3
C.2.5
D.2
B
)
A.3.5
B.3
C.2.5
D.2
答案:
6. B
7. (2023·贾汪期中)如图,点$B,C,D$在同一条直线上,$AC=BE,AC \perp BE,\angle ABC=\angle D=90^{\circ},AB=12,DE=5$,则$CD=$

7
.
答案:
7. 7
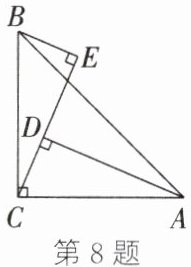
8. 如图,$\angle ACB=90^{\circ},AC=BC,BE \perp CE$于点$E,AD \perp CE$于点$D$. 有下列结论: ①$\angle ABE=\angle BAD$; ②$\triangle CEB\cong\triangle ADC$; ③$AB=CE$; ④$AD-BE=DE$. 其中,正确的是(填序号).

答案:
8. ①②④
查看更多完整答案,请扫码查看


