《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

9. 如图，$\triangle ABC$，$\triangle CDE$ 均为等边三角形，连接 $BD$，$AE$ 交于点 $O$，$BC$ 与 $AE$ 交于点 $P$，则$\angle AOB$ 的度数是60°。

答案： 9.60°

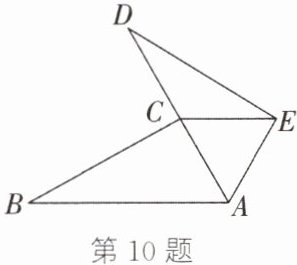
10. 如图，点 $C$ 在线段 $AD$ 上，$AB = AD$，$\angle B = \angle D$，$BC = DE$。
（1）求证：$AC = AE$；
（2）若 $CE// AB$，求$\angle BAC$ 的度数。

答案： 10.
(1) 在 △ABC 和 △ADE 中，$\begin{cases} AB = AD, \\ ∠B = ∠D, \\ BC = DE, \end{cases} $
∴△ABC ≌ △ADE(SAS).
∴ AC = AE
(2)
∵ CE // AB,
∴ ∠BAC = ∠ACE.
∵ △ABC ≌ △ADE,
∴ ∠BAC = ∠CAE, AC = AE.
∴ ∠CEA = ∠ACE.
∴ ∠CAE = ∠CEA = ∠ACE，即 △ACE 是等边三角形.
∴ ∠BAC = ∠CAE = 60°

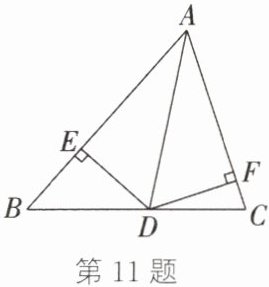
11. 如图，在$\triangle ABC$ 中，$\angle BAC = 60^{\circ}$，点 $D$ 在 $BC$ 上，$AD = 9$，$DE\perp AB$，$DF\perp AC$，垂足分别为 $E$，$F$，且 $DE = DF$。求 $DE$ 的长。

答案： 11.
∵ DE ⊥ AB, DF ⊥ AC, DE = DF, ∠BAC = 60°,
∴$ ∠BAD = ∠CAD = \frac{1}{2} ∠BAC = 30°. $在 Rt △ADE 中，∠BAD = 30°, AD = 9,
∴$ DE = \frac{1}{2} AD = 4.5$

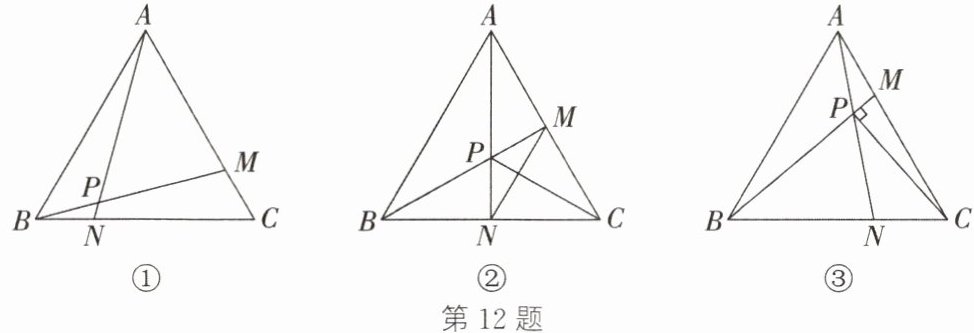
12. 在等边三角形 $ABC$ 中，点 $M$，$N$ 分别在 $AC$，$BC$ 上，且 $CM = BN$，连接 $BM$ 与 $AN$ 交于点 $P$。
（1）如图①，若$\angle CBM = 15^{\circ}$，求$\angle ANC$ 的度数；
（2）如图②，连接 $CP$，$MN$，当 $BP = CP$ 时，求证：$CP$ 是 $MN$ 的垂直平分线；
（3）如图③，连接 $CP$，当 $CP\perp BM$ 时，若 $AP = 1$，求 $BP$ 的长。

答案：
12.
(1)
∵△ABC是等边三角形，
∴AB=BC=AC,∠ABC=∠BCA=60°.在△ABN和△BCM中，$\begin{cases} AB = BC, \\ ∠ABN = ∠C, \\ BN = CM, \end{cases} $
∴△ABN≌△BCM(SAS).
∴∠BAN = ∠CBM = 15°.
∴∠ANC = ∠ABC + ∠BAN = 60° + 15° = 75°
(2)
∵△ABC是等边三角形，
∴AB=AC=BC.
∵BP=CP,
∴AN垂直平分BC.
∴BN=CN.
∵BN=CM,
∴CN=CM.
∴BN=CN=CM=AM.
∴BM⊥AC.在△APM和△BPN中，$\begin{cases} ∠AMP = ∠BNP = 90°, \\ ∠APM = ∠BPN, \\ AM = BN, \end{cases} $
∴△APM≌△BPN (AAS).
∴ PN = PM.
∵ CN = CM,
∴ CP 是 MN 的垂直平分线
(3)如图，过点B作BH⊥AN于点H.
∵CP⊥BM,
∴∠BHA = ∠BPC = 90°.由
(1)知，∠BAN = ∠CBM.在△ABH和△BCP中，$\begin{cases} ∠BHA = ∠CPB, \\ ∠BAH = ∠CBP, \\ AB = BC, \end{cases} $
∴△ABH≌△BCP (AAS).
∴ AH = BP.
∵△ABC是等边三角形，
∴AB=AC=BC,∠BAC = ∠ABC = ∠ACB = 60°.
∵BN = CM,
∴CN = AM.在△ABM和△CAN中，$\begin{cases} AB = CA, \\ ∠BAM = ∠ACN, \\ AM = CN, \end{cases} $
∴△ABM≌△CAN (SAS).
∴ ∠ABM = ∠CAN.
∴ ∠BPH = ∠ABM + ∠BAP = ∠CAN + ∠BAP = 60°.
∴ ∠PBH = 90° - ∠BPH = 30°.
∴ BP = 2PH.
∵ AH = BP = AP + PH = 2PH,
∴ PH = AP = 1.
∴ BP = 2