第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 下列说法中,正确的是(
A.带根号的数是无理数
B.无理数不能在数轴上表示出来
C.无理数是无限小数
D.无限小数是无理数
C
)A.带根号的数是无理数
B.无理数不能在数轴上表示出来
C.无理数是无限小数
D.无限小数是无理数
答案:
1. C
2. 如图,数轴上表示$\sqrt{2}$的点可能是(

A.$A$
B.$B$
C.$C$
D.$D$
C
)
A.$A$
B.$B$
C.$C$
D.$D$
答案:
2. C
$3. $数轴上表示$-\sqrt{5}$的点到原点的距离为
$\sqrt{5}$
$.$
答案:
$3. \sqrt{5}$
4.(教材P74练习T1变式)把下列各数填到相应的括号内(填序号).
①$\sqrt{12}$;②$-\frac{1}{3}$;③$\sqrt[3]{-8}$;④$0.54$;⑤$0.\dot{1}\dot{3}$;⑥$\frac{\pi}{9}$;⑦$0$;⑧$-23$;⑨$(\sqrt{7})^{2}$;⑩$0.2020020002\cdots$(相邻两个$2$之间$0$的个数逐次加$1$).
有理数:$\{\cdots\}$;
无理数:$\{\cdots\}$;
正实数:$\{\cdots\}$;
负实数:$\{\cdots\}$.
①$\sqrt{12}$;②$-\frac{1}{3}$;③$\sqrt[3]{-8}$;④$0.54$;⑤$0.\dot{1}\dot{3}$;⑥$\frac{\pi}{9}$;⑦$0$;⑧$-23$;⑨$(\sqrt{7})^{2}$;⑩$0.2020020002\cdots$(相邻两个$2$之间$0$的个数逐次加$1$).
有理数:$\{\cdots\}$;
无理数:$\{\cdots\}$;
正实数:$\{\cdots\}$;
负实数:$\{\cdots\}$.
答案:
4. ②③④⑤⑦⑧⑨ ①⑥⑩ ①④⑤⑥⑨⑩ ②③⑧
5.(数形结合思想)实数$a$,$b$,$c$在数轴上的位置如图所示,化简$\sqrt{(a - b)^{2}}-\vert a + c\vert+\sqrt{(b - c)^{2}}$.


答案:
5. 由数轴,得$ c<a<0,b>0,\therefore a - b<0,a + c<0,b - c>0.$
$\therefore \sqrt{(a - b)^2} - $|a + c|$ + \sqrt{(b - c)^2} = $|a - b| - |a + c| +
|b - c| = (b - a) - (-a - c) + (b - c) = b - a + a + c + b -
c = 2b
$\therefore \sqrt{(a - b)^2} - $|a + c|$ + \sqrt{(b - c)^2} = $|a - b| - |a + c| +
|b - c| = (b - a) - (-a - c) + (b - c) = b - a + a + c + b -
c = 2b
6. 在$0$,$2$,$-\sqrt{3}$,$\pi$四个数中,最小的数是(
A.$0$
B.$2$
C.$-\sqrt{3}$
D.$\pi$
C
)A.$0$
B.$2$
C.$-\sqrt{3}$
D.$\pi$
答案:
6. C
7. 如图,$x^{2}=3$,则在数轴上与实数$x$对应的点可能是(
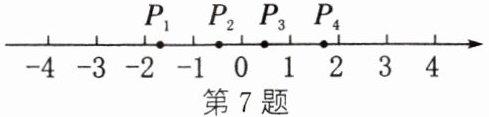
A.$P_{1}$
B.$P_{4}$
C.$P_{2}$或$P_{3}$
D.$P_{1}$或$P_{4}$
D
)
A.$P_{1}$
B.$P_{4}$
C.$P_{2}$或$P_{3}$
D.$P_{1}$或$P_{4}$
答案:
7. D
8.(2023·徐州二模)若$\sqrt{2}<a<\pi$,则下列结论正确的是(
A.$1 < a < 3$
B.$1 < a < 4$
C.$2 < a < 3$
D.$2 < a < 4$
B
)A.$1 < a < 3$
B.$1 < a < 4$
C.$2 < a < 3$
D.$2 < a < 4$
答案:
8. B
查看更多完整答案,请扫码查看


