《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

9. 在一个直角三角形中，已知一条直角边是$3\mathrm{cm}$，斜边上的中线为$2.5\mathrm{cm}$，则这个直角三角形的面积为6$\mathrm{cm}^{2}$.

答案： 9. 6

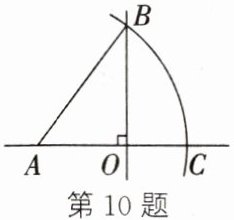
10. 如图，直线$AO\perp OB$，垂足为$O$，线段$AO = 6$，$BO = 8$.若以点$A$为圆心，$AB$的长为半径作弧，交直线$AO$于点$C$，且点$C$在点$O$的右侧，则$OC =$4.

答案： 10. 4

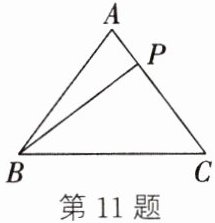
$11. $如图，在$\triangle ABC$中，点$P$在边$AC$上移动$.$若$AB = AC = 5，$$BC = 6，$则$AP + BP + CP$的最小值为　　$\frac{49}{5}$　　$.$　　

答案： $11. \frac{49}{5}$

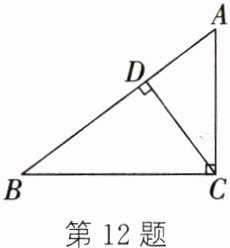
12. 如图，在$\triangle ABC$中，$\angle ACB = 90^{\circ}$，$CD\perp AB$，垂足为$D$，$AC = 9\mathrm{cm}$，$BC = 12\mathrm{cm}$.求：
（1）$AB$的长；
（2）斜边$AB$上的高$CD$的长.

答案： 12.
(1)
∵ 在 △ABC 中，∠ACB = 90°,
∴ 由勾股定理，得 AB² = AC² + BC².
∵ AC = 9 cm，BC = 12 cm，
∴ AB = 15 cm
(2)
∵ CD ⊥ AB，
∴$ S△ABC = \frac{1}{2}AC·BC = \frac{1}{2}AB·CD.$
∴$ CD = \frac{AC·BC}{AB} = \frac{9×12}{15} = 7.2(cm)$

13. (新考向·数学文化)勾股定理是一个基本的几何定理，在我国西汉时期算书《周髀算经》中就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数，那么这样的直角三角形叫“整数直角三角形”，这三个整数叫作一组“勾股数”.如$3$，$4$，$5$；$5$，$12$，$13$；$8$，$15$，$17$都是勾股数.
(1)如果$a$，$b$，$c$是一组勾股数，即满足$a^{2}+b^{2}=c^{2}$，那么$ka$，$kb$，$kc$($k$为正整数)也是一组勾股数.如$5$，$12$，$13$是一组勾股数，则10,24,26也是一组勾股数(写出一组即可).
(2)世界上第一次给出的勾股数公式，收集在我国的《九章算术》中，书中提到：当$a=\dfrac{1}{2}(m^{2}-n^{2})$，$b = mn$，$c=\dfrac{1}{2}(m^{2}+n^{2})$($m$，$n$为正整数，$m ＞ n$)时，$a$，$b$，$c$是一组勾股数.请证明满足以上公式的$a$，$b$，$c$是一组勾股数.

答案： 13.
(1) 答案不唯一，如 10,24,26
(2) 依题意，得$ a² + b² = [\frac{1}{2}(m² - n²)]² + (mn)² = \frac{1}{4}m⁴ - \frac{1}{2}m²n² + \frac{1}{4}n⁴ + m²n² = \frac{1}{4}m⁴ + \frac{1}{2}m²n² + \frac{1}{4}n⁴ = [\frac{1}{2}(m² + n²)]² = c²,$
∴ 满足以上公式的 a,b,c 是一组勾股数