第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. (2024·丰县期中)如图,$\triangle ABC\cong\triangle DEF$,点$B$,$F$,$C$,$E$在同一条直线上. 若$CE = 2$,则线段$BF$的长为(
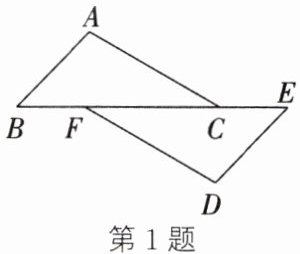
A.2
B.2.5
C.3
D.5
A
)
A.2
B.2.5
C.3
D.5
答案:
1. A
2. (2023·贾汪期中)如图,$\triangle ABC\cong\triangle ADC$,若$\angle B = 25^{\circ}$,则$\angle D$为(
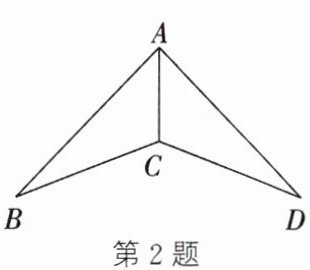
A.$20^{\circ}$
B.$25^{\circ}$
C.$30^{\circ}$
D.$50^{\circ}$
B
)
A.$20^{\circ}$
B.$25^{\circ}$
C.$30^{\circ}$
D.$50^{\circ}$
答案:
2. B
3. (2023·徐州段考)如图,$\triangle ABC\cong\triangle AEF$,有下列结论:①$AC = AF$;②$\angle FAB = \angle EAB$;③$EF = BC$;④$\angle EAB = \angle FAC$. 其中,正确的个数是(
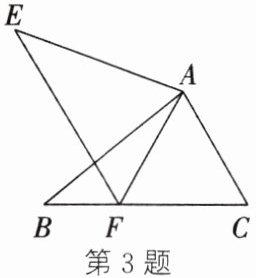
A.1
B.2
C.3
D.4
C
)
A.1
B.2
C.3
D.4
答案:
3. C
4. (2024·徐州模拟)若$\triangle ABC\cong\triangle DEF$,$AB = DE$,$BC = EF$,则$AC$的对应边是
DF
,$\angle ACB$的对应角是∠DFE
.
答案:
4. DF ∠DFE
5. (2024·南京期中改编)如图,$\triangle ABC\cong\triangle ADE$,若$\angle B = 30^{\circ}$,$\angle E = 100^{\circ}$,$\angle CAE = 40^{\circ}$,则$\angle CAD$为
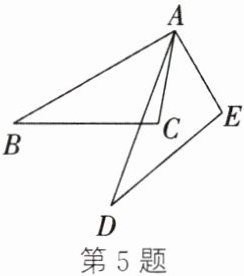
10
$^{\circ}$.
答案:
5. 10
6. (2024·邳州期中)已知$\triangle ABC\cong\triangle DEF$,$BC = EF = 4\ cm$,$\triangle ABC$的面积是$16\ cm^2$,则$\triangle DEF$的边$EF$上的高是
8
$cm$.
答案:
6. 8
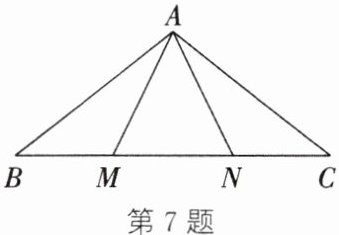
7. 如图,$\triangle ABN\cong\triangle ACM$,点$B$,$M$,$N$,$C$在同一条直线上.$\angle B$与$\angle C$是对应角,$AB$与$AC$是对应边.
(1) (教材 P13 练习 T1 变式)写出其他的对应边和对应角.
(2) 求证:①$BM = NC$;②$\angle BAM = \angle CAN$.
(1) (教材 P13 练习 T1 变式)写出其他的对应边和对应角.
(2) 求证:①$BM = NC$;②$\angle BAM = \angle CAN$.

答案:
7.
(1) 对应边:BN 与 CM,AN 与 AM;对应角:∠BAN 与 ∠CAM,∠BNA 与 ∠CMA
(2) ①
∵ △ABN ≅ △ACM,
∴ BN = CM.
∴ BN - MN = CM - MN,即 BM = NC
②
∵ △ABN ≅ △ACM,
∴ ∠BAN = ∠CAM.
∴ ∠BAN - ∠MAN = ∠CAM - ∠MAN,即∠BAM = ∠CAN
(1) 对应边:BN 与 CM,AN 与 AM;对应角:∠BAN 与 ∠CAM,∠BNA 与 ∠CMA
(2) ①
∵ △ABN ≅ △ACM,
∴ BN = CM.
∴ BN - MN = CM - MN,即 BM = NC
②
∵ △ABN ≅ △ACM,
∴ ∠BAN = ∠CAM.
∴ ∠BAN - ∠MAN = ∠CAM - ∠MAN,即∠BAM = ∠CAN
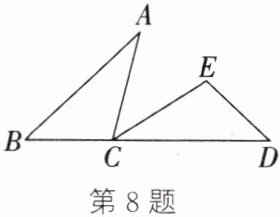
8. (2025·合肥期末)如图,点$B$,$C$,$D$在同一条直线上,若$\triangle ABC\cong\triangle CDE$,$AB = 9$,$BD = 14$,则$BC$的长为(
A.9
B.4
C.5
D.6
C
)
A.9
B.4
C.5
D.6
答案:
8. C
查看更多完整答案,请扫码查看


