《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

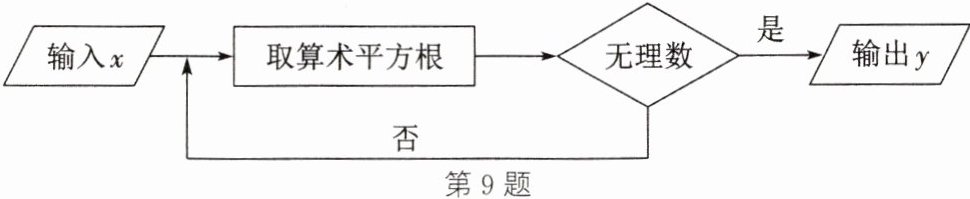
9. 如图所示为一个数值转换机，当输入的$x$的值为$81$时，则输出的$y$的值为\sqrt{3}.

答案： $9. \sqrt{3}$

10. (新情境·日常生活)某中学美术活动小组准备去郊外进行写生活动，学校为每一名同学准备了一个正方形画板（不可折叠），为了方便同学们携带，每一个画板需要放进手提袋内（假设手提袋是一个长方体，画板的厚度与手提袋的宽相等）.
【课题探究】探究画板能否直接放进手提袋内.
【相关数据】正方形画板的面积为$3600cm^{2}$，手提袋的长与高的比为$15:17$，正面面积为$6375cm^{2}$. 判断画板能否直接放进手提袋内，并说明理由.

答案： 10. 能 理由：设手提袋的长为 15x cm，高为 17x cm. 由题意，得$ 15x \cdot 17x = 6375，$解得 x = 5 或 x = -5（舍去$）. \therefore $手提袋的长为 75 cm. 由题意知，画板的边长为$ \sqrt{3600} = 60(cm). \because 75 ＞ 60, \therefore $画板能直接放进手提袋内.

11. (新视角·新定义题)任意一个无理数介于两个整数之间，我们定义，若无理数$T$满足$m ＜ T ＜ n$(其中$m$为满足不等式的最大整数，$n$为满足不等式的最小整数)，则称无理数$T$的“立信区间”为$(m,n)$，如$1 ＜ \sqrt{3} ＜ 2$，$\therefore\sqrt{3}$的“立信区间”为$(1,2)$.
(1)无理数$\sqrt{11}$的“立信区间”是(3,4)；
(2)若其中一个无理数的“立信区间”为$(m,n)$且满足$0 ＜ m+\sqrt{n} ＜ 12$，其中$\begin{cases}x = m,\\y = \sqrt{n}\end{cases}$是关于$x$，$y$的方程$mx - ny = C$的一组正整数解，求$C$的值；
(3)实数$x$，$y$，$m$满足关系式$\sqrt{2x + 3y - m}+\sqrt{3x + 4y - 2m}=\sqrt{x + y - 24}+\sqrt{24 - x - y}$，求$m$的算术平方根的“立信区间”.

答案： $11. $　　
$(1) (3,4) $　　
$(2) $由题意得，$m，$$n $是两个相邻的正整数，且$ m ＜ n.$　　
$\because \begin{cases} x = m, \\ y = \sqrt{n} \end{cases} $是关于$ x，$$y $的方程$ mx - ny = C $的一组正整数解，　　
$\therefore n $是一个完全平方数，$m ＞ 0. \because 0 ＜ m + \sqrt{n} ＜ 12, \therefore $满足题意的$ m，$$n $的值为$ 3,4 $或$ 8,9. $当$ m = 3, n = 4 $时，$\begin{cases} x = 3, \\ y = 2, \end{cases} \therefore 3 × 3 - 4 × 2 = C. \therefore C = 1; $当$ m = 8, n = 9 $时，$\begin{cases} x = 8, \\ y = 3, \end{cases} \therefore 8 × 8 - 9 × 3 = C. \therefore C = 37. $综上所述，$C $的值为$ 1 $或$ 37 (3) \because $实数$ x，$$y，$$m $满足关系式$ \sqrt{2x + 3y - m} + \sqrt{3x + 4y - 2m} = \sqrt{x + y - 24} + \sqrt{24 - x - y}, \therefore x + y - 24 \geq 0, 24 - x - y \geq 0. \therefore x + y = 24. \therefore \sqrt{2x + 3y - m} + \sqrt{3x + 4y - 2m} = 0. \because 2x + 3y - m \geq 0, 3x + 4y - 2m \geq 0, \therefore 2x + 3y - m = 0, 3x + 4y - 2m = 0, $两式相减，得$ x + y - m = 0. \therefore m = x + y = 24. \therefore m $的算术平方根为$ \sqrt{24}. \because 16 ＜ 24 ＜ 25, \therefore 4 ＜ \sqrt{24} ＜ 5. \therefore m $的算术平方根的$“$立信区间$”$是$(4,5)$