《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

8. 已知点$P(0,-4)$,$Q(6,1)$,将线段$PQ$平移至$P_1Q_1$,点$P$,$Q$的对应点分别为$P_1$,$Q_1$,若$P_1(m,-3)$,$Q_1(3,n)$,则$m - n$的值是-5。

答案： 8. -5

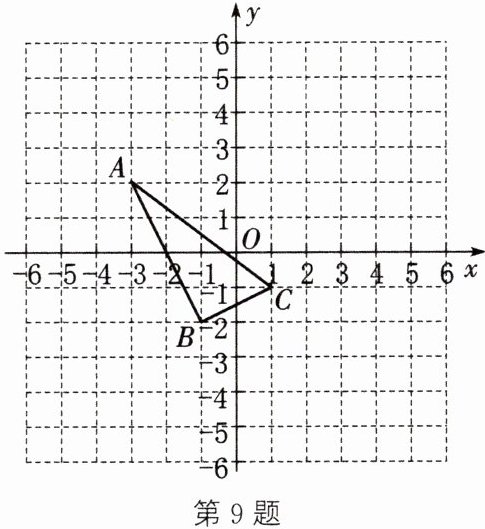
9. 如图,$A(-3,2)$,$B(-1,-2)$,$C(1,-1)$.将$\triangle ABC$先向右平移$3$个单位长度,再向上平移$1$个单位长度,可以得到$\triangle A_1B_1C_1$.
(1) $\triangle A_1B_1C_1$的顶点$A_1$的坐标为(0,3)，顶点$C_1$的坐标为(4,0)；
(2) 已知点$P$在$x$轴上,以$A_1$,$C_1$,$P$三点为顶点的三角形的面积为$3$,求点$P$的坐标.

答案： 9.
(1) (0,3) (4,0)
(2) 设点P的坐标为(t,0). 由题意，得$\frac{1}{2}$×3×|t - 4| = 3，解得t = 2或6.
∴点P的坐标为(2,0)或(6,0)

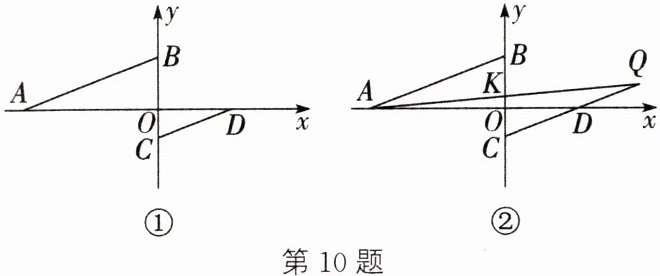
10. 如图①,在平面直角坐标系中,点$A$,$B$,$C$,$D$均在坐标轴上,其坐标分别是$A(a,0)$,$B(0,b)$,$C(0,c)$,$D(d,0)$,若$\vert a + 4\vert+\sqrt{b - 3}=0$,$c\lt0$,$d\gt0$,且$\angle ABO=\angle DCO$.
(1) 求$\triangle AOB$的面积；
(2) 求证:$3d=-4c$；
(3) 如图②,若$-3\lt c\lt0$,延长$CD$到点$Q$,使$CQ = AB$,线段$AQ$交$y$轴于点$K$,求$\frac{BK - OK}{OC}$的值.

答案：
10.
(1)
∵ |a + 4| + $\sqrt{b - 3}$ = 0，
∴ a = -4，b = 3.
∴ A(-4,0)，B(0,3).
∴ AO = 4，BO = 3.
∴ S_{△AOB} = $\frac{1}{2}$×4×3 = 6
(2) 如图①，连接AC，BD.
∵ ∠ABO = ∠DCO，
∴ AB//CD.
∴ S_{△ABC} = S_{△ABD}.
∴ $\frac{1}{2}$BC·AO = $\frac{1}{2}$AD·BO.
∴ $\frac{1}{2}$×(3 - c)×4 = $\frac{1}{2}$×(4 + d)×3.
∴ 3d = -4c
(3) 如图②，连接OQ.
∵ AB = CQ，AB//CQ，
∴ 线段CQ可看作是由线段AB平移得到的.
∵ 点A(-4,0)平移得到点C(0,c)，
∴ 点B(0,3)平移得到点Q(4,3 + c). 设点K的坐标为(0,y)，则S_{△AOQ} = $\frac{1}{2}$×4×(3 + c) = 2(3 + c)，S_{△AOK} = 2y，S_{△QOK} = 2y.
∵ S_{△AOQ} = S_{△AOK} + S_{△QOK}，
∴ 2y + 2y = 2(3 + c)，解得y = $\frac{3 + c}{2}$.
∴ BK = 3 - $\frac{3 + c}{2}$ = $\frac{3 - c}{2}$，OK = $\frac{3 + c}{2}$，OC = -c.
∴ $\frac{BK - OK}{OC}$ = 1