第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
9. 如图,在平面直角坐标系中,$ A,B $ 两点的坐标分别为$ (a,7),(5,b) $,则点 $ C(6 - a,b - 10) $ 在此坐标系中位于(
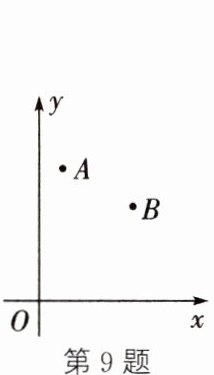
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
9.D
10. 在平面直角坐标系中,$ O $ 是坐标原点,点 $ A $ 的坐标为$ (-5,12) $,则 $ OA $ 的长为
13
.
答案:
10.13
11. 如图,所有正方形的中心均为坐标原点,且各边与 $ x $ 轴或 $ y $ 轴平行,从内到外,它们的边长依次为 $ 4,6,8,\cdots $,顶点依次为 $ A_1,A_2,A_3,A_4,\cdots $,则顶点 $ A_{2025} $ 的坐标是
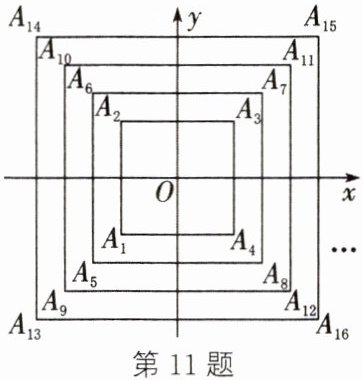
(-508,-508)
.
答案:
11.(-508,-508)
12. (教材 $ P115 $ 练习 $ T1 $ 变式)如图,写出多边形 $ ABCDE $ 各个顶点的坐标,它们的坐标分别为 $ A $
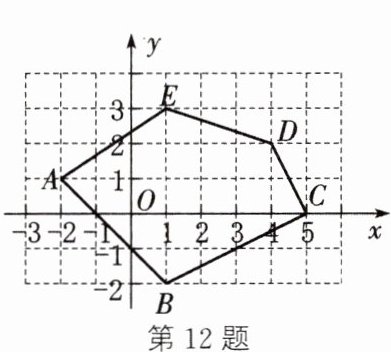
(-2,1)
,$ B $(1,-2)
,$ C $(5,0)
,$ D $(4,2)
,$ E $(1,3)
.
答案:
12.(-2,1) (1,-2) (5,0) (4,2) (1,3)
13. (教材 $ P115 $ 练习 $ T2 $ 变式)已知四边形 $ OACB $ 的四个顶点分别是$ O(0,0),B(3,6),C(9,8),A(11,0) $.在如图所示的平面直角坐标系中画出这个四边形,并求这个四边形的面积.


答案:
13.如图,四边形OACB即为所求作 如图,分别过点B,C作BD⊥x轴,CE⊥x轴,垂足分别为D,E,
∴S四边形OACB=S△OBD+S梯形BCED+S△ACE=1/2×3×6+1/2×(6+8)×6+1/2×2×8=9+42+8=59

13.如图,四边形OACB即为所求作 如图,分别过点B,C作BD⊥x轴,CE⊥x轴,垂足分别为D,E,
∴S四边形OACB=S△OBD+S梯形BCED+S△ACE=1/2×3×6+1/2×(6+8)×6+1/2×2×8=9+42+8=59

14. 已知在平面直角坐标系中有三点 $ A(-2,1),B(3,1),C(2,3) $,请回答如下问题:
(1)在如图所示的平面直角坐标系中描出点 $ A,B,C $ 的位置,连接 $ AB,AC,BC $,则$ \triangle ABC $ 是
(2)$ \triangle ABC $ 的面积是
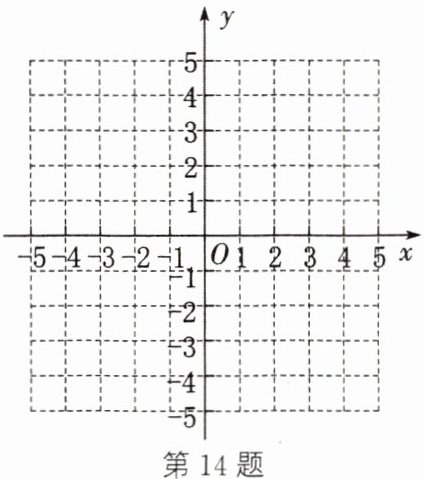
(1)在如图所示的平面直角坐标系中描出点 $ A,B,C $ 的位置,连接 $ AB,AC,BC $,则$ \triangle ABC $ 是
直角
三角形;(2)$ \triangle ABC $ 的面积是
5
.
答案:
14.
(1)如图,△ABC即为所求作 直角
(2)5

14.
(1)如图,△ABC即为所求作 直角
(2)5

查看更多完整答案,请扫码查看


