第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. (新考向·数学文化)我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理,体现了我国古代的数学成就. 如图所示的“弦图”是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形. 直角三角形的斜边长为 13,一条直角边长为 12,则小正方形 $ABCD$ 的面积是(
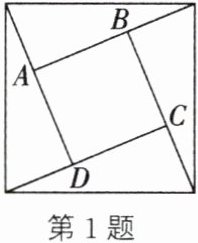
A.25
B.36
C.49
D.64
C
)
A.25
B.36
C.49
D.64
答案:
1. C
2. (新情境·日常生活)为了强化实践育人,有效开展劳动教育和综合实践活动,某校校园里现有一块四边形的空地 $ABCD$, 如图所示, 学校决定开发该空地作为学生劳动实践基地. 经学校课外实践活动小组测量得到: $\angle BAD = 90^{\circ}$, $AD = 3m$, $AB = 4m$, $BC = 13m$, $CD = 12m$. 根据你所学过的知识解决以下问题:
(1) 求证: $\angle BDC = 90^{\circ}$;
(2) 求四边形 $ABCD$ 的面积.
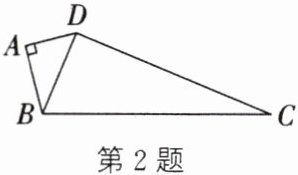
(1) 求证: $\angle BDC = 90^{\circ}$;
(2) 求四边形 $ABCD$ 的面积.

答案:
2.
(1) $\because \angle BAD = 90°$, $AD = 3\ m$, $AB = 4\ m$, $\therefore BD = \sqrt{AD^2 + AB^2} = \sqrt{3^2 + 4^2} = 5(m)$. $\because BC = 13\ m$, $CD = 12\ m$, $\therefore BD^2 + CD^2 = 5^2 + 12^2 = 169(m^2)$, $BC^2 = 13^2 = 169(m^2)$. $\therefore BD^2 + CD^2 = BC^2$. $\therefore \triangle BCD$ 是直角三角形. $\therefore \angle BDC = 90°$.
(2) 四边形 $ABCD$ 的面积 $= \triangle ABD$ 的面积 $+ \triangle BCD$ 的面积 $= \frac{1}{2} AD \cdot AB + \frac{1}{2} BD \cdot CD = \frac{1}{2} × 3 × 4 + \frac{1}{2} × 5 × 12 = 6 + 30 = 36(m^2)$.
(1) $\because \angle BAD = 90°$, $AD = 3\ m$, $AB = 4\ m$, $\therefore BD = \sqrt{AD^2 + AB^2} = \sqrt{3^2 + 4^2} = 5(m)$. $\because BC = 13\ m$, $CD = 12\ m$, $\therefore BD^2 + CD^2 = 5^2 + 12^2 = 169(m^2)$, $BC^2 = 13^2 = 169(m^2)$. $\therefore BD^2 + CD^2 = BC^2$. $\therefore \triangle BCD$ 是直角三角形. $\therefore \angle BDC = 90°$.
(2) 四边形 $ABCD$ 的面积 $= \triangle ABD$ 的面积 $+ \triangle BCD$ 的面积 $= \frac{1}{2} AD \cdot AB + \frac{1}{2} BD \cdot CD = \frac{1}{2} × 3 × 4 + \frac{1}{2} × 5 × 12 = 6 + 30 = 36(m^2)$.
3. 如图, 经过 $A$ 村和 $B$ 村(将 $A$, $B$ 村看成直线 $l$ 上的点) 的笔直公路 $l$ 旁有一块山地正在开发, 现需要在点 $C$ 处进行爆破. 已知点 $C$ 处与 $A$ 村的距离为 900 米, 点 $C$ 处与 $B$ 村的距离为 1200 米,且 $AC \perp BC$.
(1) 求 $A$, $B$ 两村之间的距离.
(2) 求点 $C$ 到直线 $l$ 的距离.
(3) 为了安全起见, 爆破点 $C$ 周围半径 750 米范围内不得进入, 在进行爆破时, $A$, $B$ 两村间的公路是否有危险而需要封锁? 如果需要, 请计算需要封锁的路段长度; 如果不需要, 请说明理由.
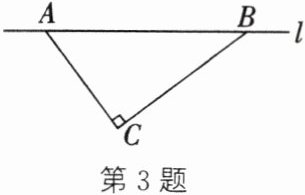
(1) 求 $A$, $B$ 两村之间的距离.
(2) 求点 $C$ 到直线 $l$ 的距离.
(3) 为了安全起见, 爆破点 $C$ 周围半径 750 米范围内不得进入, 在进行爆破时, $A$, $B$ 两村间的公路是否有危险而需要封锁? 如果需要, 请计算需要封锁的路段长度; 如果不需要, 请说明理由.

答案:
3.
(1) 在 $Rt \triangle ABC$ 中, $AC = 900$ 米, $BC = 1200$ 米, $\therefore AB = \sqrt{AC^2 + BC^2} = \sqrt{900^2 + 1200^2} = 1500$ 米, 即 $A$, $B$ 两村之间的距离为 $1500$ 米.
(2) 如图, 过点 $C$ 作 $CD \perp AB$ 于点 $D$. $\because S_{\triangle ABC} = \frac{1}{2} AB \cdot CD = \frac{1}{2} BC \cdot AC$, $\therefore CD = \frac{AC \cdot BC}{AB} = \frac{900 × 1200}{1500} = 720$ 米, 即点 $C$ 到直线 $l$ 的距离为 $720$ 米.
(3) $A$, $B$ 两村间的公路有危险而需要封锁. $\because 720 < 750$, $\therefore$ 有危险. $\therefore A$, $B$ 两村间的公路需要封锁. 如图, 以点 $C$ 为圆心, $750$ 米为半径画弧, 交 $AB$ 于点 $E$, $F$, 连接 $CE$, $CF$, $\therefore EC = FC = 750$ 米. $\therefore ED = \sqrt{750^2 - 720^2} = 210$ 米. $\because \triangle CEF$ 是等腰三角形, $\therefore DE = DF = \frac{1}{2} EF$. $\therefore EF = 2DE = 420$ 米, 即需要封锁的路段长度为 $420$ 米.

3.
(1) 在 $Rt \triangle ABC$ 中, $AC = 900$ 米, $BC = 1200$ 米, $\therefore AB = \sqrt{AC^2 + BC^2} = \sqrt{900^2 + 1200^2} = 1500$ 米, 即 $A$, $B$ 两村之间的距离为 $1500$ 米.
(2) 如图, 过点 $C$ 作 $CD \perp AB$ 于点 $D$. $\because S_{\triangle ABC} = \frac{1}{2} AB \cdot CD = \frac{1}{2} BC \cdot AC$, $\therefore CD = \frac{AC \cdot BC}{AB} = \frac{900 × 1200}{1500} = 720$ 米, 即点 $C$ 到直线 $l$ 的距离为 $720$ 米.
(3) $A$, $B$ 两村间的公路有危险而需要封锁. $\because 720 < 750$, $\therefore$ 有危险. $\therefore A$, $B$ 两村间的公路需要封锁. 如图, 以点 $C$ 为圆心, $750$ 米为半径画弧, 交 $AB$ 于点 $E$, $F$, 连接 $CE$, $CF$, $\therefore EC = FC = 750$ 米. $\therefore ED = \sqrt{750^2 - 720^2} = 210$ 米. $\because \triangle CEF$ 是等腰三角形, $\therefore DE = DF = \frac{1}{2} EF$. $\therefore EF = 2DE = 420$ 米, 即需要封锁的路段长度为 $420$ 米.

查看更多完整答案,请扫码查看


