《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

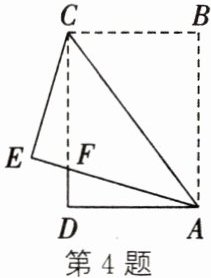
4. (2024·丰县段考) 如图, 在长方形纸片 $ABCD$ 中, $AB = 8cm$, $AD = 6cm$. 把长方形纸片沿直线 $AC$ 折叠, 使点 $B$ 落在点 $E$ 处, $AE$ 交 $DC$ 于点 $F$, 则 $AF$ 的长为(A)

A.$\frac{25}{4}cm$
B.$\frac{15}{2}cm$
C.$7cm$
D.$\frac{13}{2}cm$

答案： 4. A

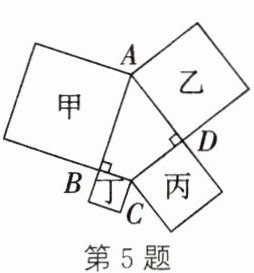
5. (2025·邳州期中) 如图, 在四边形 $ABCD$ 中, $\angle ABC = \angle ADC = 90^{\circ}$, 分别以 $AB$, $BC$, $CD$, $DA$ 为边向外作正方形. 若乙的面积是 25, 丙的面积是 15, 丁的面积是 4, 则 $AB =$6.

答案： 5. 6

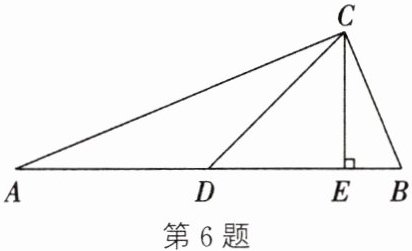
6. (2024·邳州期中) 如图, $CD$ 是 $\triangle ABC$ 的中线, $CE$ 是 $\triangle ABC$ 的高, $AC = 12cm$, $BC = 5cm$, $AB = 13cm$. 求:
(1) 高 $CE$ 的长;
(2) $\triangle ACD$ 的面积.

答案： 6.
(1) $\because AC = 12\ cm$, $BC = 5\ cm$, $AB = 13\ cm$, $\therefore AC^2 + BC^2 = 12^2 + 5^2 = 169(cm^2)$, $AB^2 = 13^2 = 169(cm^2)$. $\therefore AC^2 + BC^2 = AB^2$. $\therefore \triangle ABC$ 是直角三角形, 且 $\angle ACB = 90°$. $\therefore S_{\triangle ABC} = \frac{1}{2} AC \cdot BC = \frac{1}{2} AB \cdot CE$. $\therefore CE = \frac{AC \cdot BC}{AB} = \frac{60}{13}\ cm$. $\therefore$ 高 $CE$ 的长为 $\frac{60}{13}\ cm$.
(2) $\because CD$ 是 $\triangle ABC$ 的中线, $\therefore S_{\triangle ACD} = \frac{1}{2} S_{\triangle ABC} = \frac{1}{2} × \frac{1}{2} AC \cdot BC = \frac{1}{4} × 12 × 5 = 15(cm^2)$.

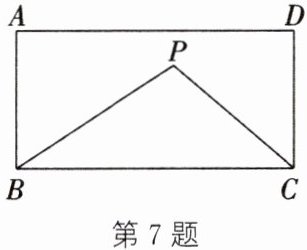
7. (2024·苏州期中) 如图, $P$ 是长方形 $ABCD$ 内部的动点, $AB = 4$, $BC = 8$, $\triangle PBC$ 的面积为 12,则点 $P$ 到 $B$, $C$ 两点距离之和 $PB + PC$ 的最小值为(C)

A.8
B.9
C.10
D.11

答案： 7. C

8. (2025·盐城期末) 图①是某品牌婴儿车, 图②为其简化结构示意图. 现测得 $AB = CD = 8dm$, $BC = 4dm$, $AD = 12dm$, 其中 $AB$ 与 $BD$ 之间由一个固定角为 $90^{\circ}$ 的零件连接 (即 $\angle ABD = 90^{\circ}$). 根据安全标准需满足 $BC \perp CD$, 请你通过计算说明该品牌婴儿车是否符合安全标准.

答案： 8. $\because \angle ABD = 90°$, $\therefore$ 在 $Rt \triangle ABD$ 中, 由勾股定理, 得 $AB^2 + BD^2 = AD^2$, $\therefore 8^2 + BD^2 = 12^2$. $\therefore BD^2 = 80\ dm^2$. $\because BC^2 + CD^2 = 4^2 + 8^2 = 80(dm^2)$, $\therefore BC^2 + CD^2 = BD^2$. $\therefore \angle BCD = 90°$, 即 $BC \perp CD$. $\therefore$ 该品牌婴儿车符合安全标准.