《2025年金钥匙提优训练课课练八年级数学上册苏科版徐州专版》

13. 定义一种叫作“*”的运算:对于任意的两个数m,n,有m*n=$m^{2}-n^{2}$,例如5*3=$5^{2}-3^{2}$=16.请解方程:x*(-1)=4*2.

答案： 13. 由题意，得$x^{2}-(-1)^{2}=4^{2}-2^{2}$，即$x^{2}-1=12$，解得$x=\pm\sqrt{13}$

14. 已知5x-1的平方根是±3,4x+2y+1的平方根是±1,求4x-2y的平方根.

答案： 14. 由题意，得$\begin{cases}5x - 1 = 9,\\4x + 2y + 1 = 1,\end{cases}$解得$\begin{cases}x = 2,\\y = -4.\end{cases}$ $\therefore 4x - 2y = 16$。
$\therefore 4x - 2y$的平方根为$\pm4$。

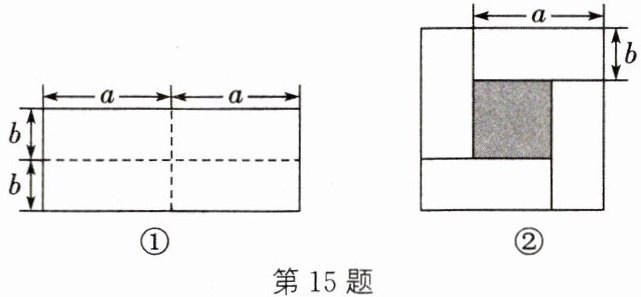
15. (数形结合思想)如图①所示为一个长为2a、宽为2b的长方形,沿图中虚线剪开分成四个小长方形,然后按如图②所示的方式拼成一个大正方形.
(1) 图②中的涂色部分的正方形的边长是$a - b$.
(2) 用两种不同的方法求图②中涂色部分的面积.
方法1:$S_{涂色}$=$(a - b)^{2}$;
方法2:$S_{涂色}$=$(a + b)^{2}-4ab$.
(3) 若a＞b,且a+b=3,ab=1,则a-b=$\sqrt{5}$.

答案： 15.
(1) $a - b$
(2) $(a - b)^{2}$ $(a + b)^{2}-4ab$ 解析：方法1：利用面积公式可得$S_{涂色}=(a - b)^{2}$；方法2：利用大正方形的面积减去四个小长方形的面积，可得$S_{涂色}=(a + b)^{2}-4ab$。
(3) $\sqrt{5}$ 解析：由
(2)，可得$S_{涂色}=(a + b)^{2}-4ab=(a - b)^{2}$。
$\because a + b = 3$，$ab = 1$，$\therefore 3^{2}-4×1 = 5=(a - b)^{2}$，解得$a - b=\pm\sqrt{5}$。$\because a＞b$，$\therefore a - b＞0$。$\therefore a - b=\sqrt{5}$。