第96页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
活动 1 生活中的阶梯计价问题
“绿色环保,人人有责;节约用水,共创美好明天.”某市为了加强公民的节水意识,合理利用水资源,采用价格调控的手段以达到节水的目的,经物价部门审核,该市自来水收费的价目表如下,请根据表中的信息解答下列问题:
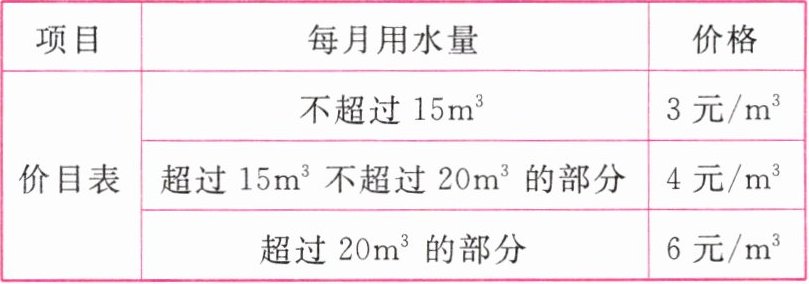
(1)若某用户 5 月份用水 $12m^3$,则应交水费______元.
(2)若该用户 7 月份应交水费 77 元,则用水______ $m^3$.
(3)若该用户 9,10 两个月共用水 $30m^3$,共交水费 93 元(9 月份用水量超过了 10 月份),求 9 月份用水量.
“绿色环保,人人有责;节约用水,共创美好明天.”某市为了加强公民的节水意识,合理利用水资源,采用价格调控的手段以达到节水的目的,经物价部门审核,该市自来水收费的价目表如下,请根据表中的信息解答下列问题:

(1)若某用户 5 月份用水 $12m^3$,则应交水费______元.
(2)若该用户 7 月份应交水费 77 元,则用水______ $m^3$.
(3)若该用户 9,10 两个月共用水 $30m^3$,共交水费 93 元(9 月份用水量超过了 10 月份),求 9 月份用水量.
答案:
36
@@22
@@设 9 月份用水 $ x\,m^3 $,则 10 月份用水$(30-x)\,m^3$.
∵9 月份用水量超过了 10 月份,
∴9 月份用水量大于 $ 15\,m^3 $,10 月份用水量小于 $ 15\,m^3 $.①当 $ 15 < x \leqslant 20 $ 时,9 月份水费:$ 15× 3+(x-15)× 4=4x-15 $,10 月份水费:$ 3(30-x)=-3x+90 $,则 $ 4x-15+(-3x+90)=93 $,解得 $ x=18 $.②当 $ 20 < x \leqslant 30 $ 时,9 月份水费:$ 15× 3+5× 4+6(x-20)=6x-55 $,10 月份水费:$ -3x+90 $,则 $ (6x-55)+(-3x+90)=93 $,解得 $ x=\dfrac{58}{3} $,不符合题意,舍去.答:9 月份用水量是 $ 18\,m^3 $.
@@22
@@设 9 月份用水 $ x\,m^3 $,则 10 月份用水$(30-x)\,m^3$.
∵9 月份用水量超过了 10 月份,
∴9 月份用水量大于 $ 15\,m^3 $,10 月份用水量小于 $ 15\,m^3 $.①当 $ 15 < x \leqslant 20 $ 时,9 月份水费:$ 15× 3+(x-15)× 4=4x-15 $,10 月份水费:$ 3(30-x)=-3x+90 $,则 $ 4x-15+(-3x+90)=93 $,解得 $ x=18 $.②当 $ 20 < x \leqslant 30 $ 时,9 月份水费:$ 15× 3+5× 4+6(x-20)=6x-55 $,10 月份水费:$ -3x+90 $,则 $ (6x-55)+(-3x+90)=93 $,解得 $ x=\dfrac{58}{3} $,不符合题意,舍去.答:9 月份用水量是 $ 18\,m^3 $.
若工人师傅欲用撬棍撬动一块大石头[如图 5-1②所示],已知阻力和阻力臂不变,分别为 $1500N$ 和 $0.4m$.
(1)动力 $F(N)$ 与动力臂 $l(m)$ 有怎样的关系?当动力臂为 $1.5m$ 时,撬动石头需要多大的力?
(2)若想使动力 $F(N)$ 等于 $200N$,则动力臂要加长多少?
(1)动力 $F(N)$ 与动力臂 $l(m)$ 有怎样的关系?当动力臂为 $1.5m$ 时,撬动石头需要多大的力?
(2)若想使动力 $F(N)$ 等于 $200N$,则动力臂要加长多少?
答案:
(1)$ F=\dfrac{600}{l} $ 撬动石头需要 400N 的力.
(2)动力臂要加长 1.5m.
(1)$ F=\dfrac{600}{l} $ 撬动石头需要 400N 的力.
(2)动力臂要加长 1.5m.
【数学思考】
(3)请用数学知识解释:我们使用撬棍,当阻力与阻力臂一定时,为什么动力臂越长越省力.
(3)请用数学知识解释:我们使用撬棍,当阻力与阻力臂一定时,为什么动力臂越长越省力.
答案:
因为撬棍工作原理遵循"杠杆定律",当阻力与阻力臂一定时,其乘积为常数,设其为 $ k $,则动力 $ F $ 与动力臂 $ l $ 的关系式为 $ F=\dfrac{k}{l} $,根据反比例关系的性质可知,动力 $ F $ 随动力臂 $ l $ 的增大而减小,所以动力臂越长越省力.
查看更多完整答案,请扫码查看


