《2025年三维数字课堂七年级数学上册人教版》

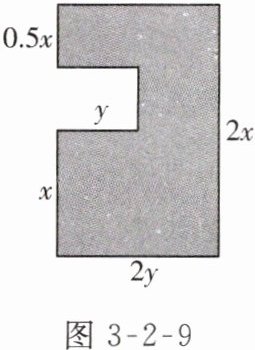
4. 【教材 P81 练习 1 变式】如图 3-2-9 所示,阴影部分图形的周长是4x+6y,当 $ x = 7 $,$ y = 3.5 $ 时,周长为49。
]

答案： $4x+6y$ 49

5. 【教材 P81 练习 3 变式】如图 3-2-10 所示,在半径为 $ R $ 的圆形钢板上,挖去半径为 $ r $ 的四个小圆,当 $ R = 7.6 \mathrm{cm} $,$ r = 1.2 \mathrm{cm} $ 时,剩余部分的面积为$52\pi$$ \mathrm{cm} ^ { 2 } $。

答案： $52\pi$

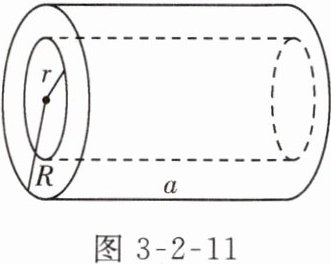
6. 【教材 P81 练习 3 变式】如图 3-2-11 所示,用式子表示图中钢管的体积。当 $ R = 12 \mathrm{cm} $,$ r = 9 \mathrm{cm} $,$ a = 20 \mathrm{cm} $ 时,求出钢管的体积($ \pi $ 取 3.14)。
]

答案： 解:图中钢管的体积为$\pi a(R^{2}-r^{2})$,当$R=12cm,r=9cm,a=20cm$时,$\pi a(R^{2}-r^{2})=3.14×20×(12^{2}-9^{2})=3956.4(cm^{3})$.故钢管的体积为$3956.4cm^{3}$.

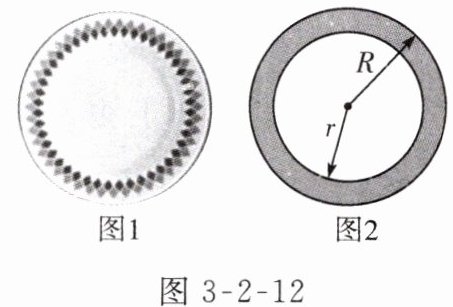
7. 【教材 P81 练习 3 变式】如图 3-2-12 所示的圆形盘子,外圆半径是 $ R \mathrm{cm} $,内圆半径是 $ r \mathrm{cm} $,现在要给盘子环形部分上釉(图 2 阴影部分),用代数式表示阴影部分的面积。当 $ R = 10.25 \mathrm{cm} $,$ r = 8.25 \mathrm{cm} $ 时,求阴影部分的面积($ \pi $ 取 3)。
]

答案： 解:由题意,得阴影部分的面积为$\pi R^{2}-\pi r^{2}$.当$R=10.25cm,r=8.25cm$时,$\pi R^{2}-\pi r^{2}=\pi×10.25^{2}-\pi×8.25^{2}=37\pi\approx111(cm^{2})$.

1. 【跨学科融合——历史】如图 3-2-13 所示,“圆形方孔钱”是中国古钱币的突出代表,一枚圆形方孔钱的外半径为 $ r $,中间方孔边长为 $ a $。
(1)用含 $ r $,$ a $ 的式子表示阴影部分的面积；
(2)当 $ r = 10 \mathrm{cm} $,$ a = 6 \mathrm{cm} $ 时,求阴影部分的面积($ \pi $ 取 3.14)。
]

答案： 解:
(1)根据题意,得阴影部分的面积为$\pi r^{2}-a^{2}$.
(2)当$r=10cm,a=6cm$时,阴影部分的面积为$\pi r^{2}-a^{2}=3.14×10^{2}-6^{2}=278(cm^{2})$.答:阴影部分的面积为$278cm^{2}$.

2. 【数图结合问题】如图 3-2-14,这是某小区的一块长为 $ b \mathrm{m} $、宽为 $ 2 a \mathrm{m} $ 的长方形草地,现在在该长方形的四个顶点处分别修建一个半径为 $ a \mathrm{m} $ 的扇形花台。
(1)求修建后剩余草坪(阴影部分)的面积(用含 $ a $,$ b $ 的代数式表示)。
(2)当 $ a = 10 $,$ b = 40 $ 时,草坪的面积是多少平方米($ \pi $ 取 3.14)？
]

答案： 解:
(1)修建后剩余草坪的面积为$2ab-4×\frac{1}{4}\pi a^{2}=2ab-\pi a^{2}(m^{2})$.
(2)当$a=10,b=40$时,$2ab-\pi a^{2}\approx2×10×40-3.14×10^{2}=800-314=486(m^{2})$.