第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
8. 下列说法:①因为相反数都是成对出现的,所以 0 没有相反数;②互为相反数的两数之和为零;③数轴上原点两侧的两点表示的数互为相反数;④若两数互为相反数,则数轴上表示它们的点与原点的距离相等。其中说法正确的有
②④
。(填序号)
答案:
②④ 点拨:①在相反数的概念中,特别规定了 0 的相反数是 0,故①不正确;②根据相反数的概念,②正确;③数轴上原点两侧的点到原点的距离不一定相等,则它们表示的数不一定互为相反数,故③不正确;④符合相反数的几何意义,故④正确.
9. 已知-2 的相反数是$x$,-5 的相反数是$y$,$z$的相反数是 0,求$x + y + z$的相反数。
答案:
解:由题意得$x = 2$,$y = 5$,$z = 0$,所以$x + y + z = 7$,所以$x + y + z$的相反数是 -7.
10. 【数形结合思想】已知数$a$、$b$表示的点在数轴上的位置如图 1-2-9 所示。
(1) 在数轴上表示出$a$、$b$的相反数的位置;
(2) 若数$b$与其相反数相距 20 个单位长度,则$b$表示的数是多少?
(3) 在(2)的条件下,若数$a表示的点与数b$的相反数表示的点相距 5 个单位长度,则$a$表示的数是多少?
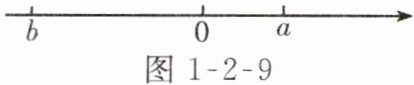
(1) 在数轴上表示出$a$、$b$的相反数的位置;
(2) 若数$b$与其相反数相距 20 个单位长度,则$b$表示的数是多少?
(3) 在(2)的条件下,若数$a表示的点与数b$的相反数表示的点相距 5 个单位长度,则$a$表示的数是多少?
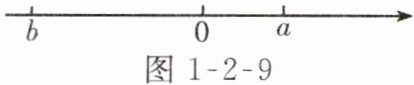
答案:
解:
(1)如答图 1 - 2 - 4 所示.

(2)因为数 b 与其相反数 -b 相距 20 个单位长度,所以 b 与 -b 到原点的距离都是 10 个单位长度. 又因为 b 在原点的左侧,所以 b 表示的数是 -10.
(3)由
(2)知 -b 与原点相距 10 个单位长度,又因为 a 与 -b 相距 5 个单位长度,且 a,-b 均在原点的右侧,所以 a 表示的数是 5.
解:
(1)如答图 1 - 2 - 4 所示.

(2)因为数 b 与其相反数 -b 相距 20 个单位长度,所以 b 与 -b 到原点的距离都是 10 个单位长度. 又因为 b 在原点的左侧,所以 b 表示的数是 -10.
(3)由
(2)知 -b 与原点相距 10 个单位长度,又因为 a 与 -b 相距 5 个单位长度,且 a,-b 均在原点的右侧,所以 a 表示的数是 5.
1. 【分类讨论思想】在数轴上点$A$表示 7,点$B$,$C$表示互为相反数的两个数,且点$C与点A$间的距离为 2,点$B$,$C$对应的数是什么?
答案:
解:因为在数轴上点 A 表示 7,点 C 与点 A 间的距离为 2,所以在数轴上点 C 表示 5 或 9. 因为点 B,C 表示互为相反数的两个数,所以在数轴上点 B 表示 -5 或 -9. 所以点 B,C 对应的数分别是 -5,5 或 -9,9.
2. 【开放推理问题】有一个“猜成语”的游戏,其规则是:参加游戏的每两人一组,主持人出示写有成语的一块牌子给两人中的一人(甲)看,但另一人(乙)是看不到牌子上的成语的,现在请甲用一句话(这句话中不能出现成语中含有的字)或一个动作告诉乙牌子上的成语,要求乙根据甲的话或动作猜出这个成语,现在我们把这个游戏中的成语改成两个整数“-1”和“1”,要求甲用一句话或者一个式子、一个图形告诉乙这两个数(同样要求不能出现牌子上的数字和符号),如果你是甲,将怎样告诉乙这两个整数?(至少说两种)
答案:
解:可以这样说:
(1)最小的正整数和它的相反数;
(2)最大的负整数和它的相反数.
点拨:本题是一道开放题,答案不唯一,合理即可.
(1)最小的正整数和它的相反数;
(2)最大的负整数和它的相反数.
点拨:本题是一道开放题,答案不唯一,合理即可.
查看更多完整答案,请扫码查看


