《2025年三维数字课堂七年级数学上册人教版》

6. 【推理问题】观察下列数据,按规律在横线上填上适当的数：$1$,$-\frac{3}{4}$,$\frac{5}{9}$,$-\frac{7}{16}$,$\frac{9}{25}$,$-\frac{11}{36}$。

答案： $-\frac{11}{36}$

7. 【推理问题】已知 $2^{1}= 2$,$2^{2}= 4$,$2^{3}= 8$,$2^{4}$ 的个位上的数是 $6$,$2^{5}$ 的个位上的数是 $2$,$2^{6}$ 的个位上的数是 $4$······则 $2^{2024}$ 的个位上的数是6。

答案： 6

8. 【跨学科融合—语文】“今有蒲生一日,长三尺；蒲生日自半。”其意思是：有蒲这种植物,蒲第一日长了 $3$ 尺,以后蒲每日生长的长度是前一日的一半。请计算出第四日后,蒲的长度为$\frac{45}{8}$尺。

答案： $\frac{45}{8}$

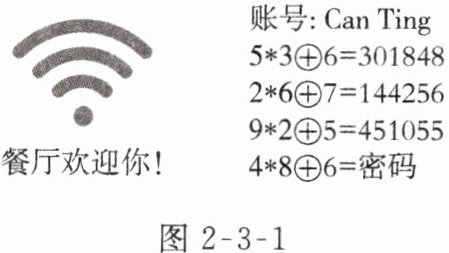
9. 【应用意识】如图 2 - 3 - 1 所示,某学校餐厅把 Wi - Fi 密码做成了数学题。小红在餐厅就餐时,思索了一会儿,输入密码,顺利地连接到了餐厅的网络。那么她输入的密码是244872。
]

答案： 244872

1. 【阅读理解问题】下面是按一定规律排列的一列数：
第 $1$ 个数：$\frac{1}{2}-\left(1+\frac{-1}{2}\right)$；
第 $2$ 个数：$\frac{1}{3}-\left(1+\frac{-1}{2}\right)\left[1+\frac{(-1)^{2}}{3}\right]\left[1+\frac{(-1)^{3}}{4}\right]$；
第 $3$ 个数：$\frac{1}{4}-\left(1+\frac{-1}{2}\right)\left[1+\frac{(-1)^{2}}{3}\right]\left[1+\frac{(-1)^{3}}{4}\right]\cdot\left[1+\frac{(-1)^{4}}{5}\right]\left[1+\frac{(-1)^{5}}{6}\right]$；
……
第 $n$ 个数：$\frac{1}{n + 1}-\left(1+\frac{-1}{2}\right)\left[1+\frac{(-1)^{2}}{3}\right]\left[1+\frac{(-1)^{3}}{4}\right]\cdot\left[1+\frac{(-1)^{4}}{5}…\right]\cdot\cdot\left[1+\frac{(-1)^{2n - 1}}{2n}\right]$。
那么在第 $10$ 个数、第 $11$ 个数、第 $12$ 个数、第 $13$ 个数中,最大的数是(A)
A.第 $10$ 个数
B.第 $11$ 个数
C.第 $12$ 个数
D.第 $13$ 个数

答案： A 点拨:仔细算一下前三个算式的结果,第1个是$\frac{1}{2}-\frac{1}{2}$,第2个是$\frac{1}{3}-\frac{1}{2}$,第3个是$\frac{1}{4}-\frac{1}{2}$,由此推出第10,11,12,13个数分别为$\frac{1}{11}-\frac{1}{2}$,$\frac{1}{12}-\frac{1}{2}$,$\frac{1}{13}-\frac{1}{2}$,$\frac{1}{14}-\frac{1}{2}$.故正确答案为A.

2. 【推理问题】【尝试】(1) 比较大小(用“$＞$”“$＜$”“$=$”“$\geqslant$”或“$\leqslant$”填空)：
① $|-2|+|3|$＞$|-2 + 3|$；
② $|-6|+|4|$＞$|-6 + 4|$；
③ $|-3|+|-4|$=$|-3 - 4|$；
④ $|0|+|-7|$=$|0 - 7|$。
【归纳】(2) 观察上面的数量关系,可以得到 $|a|+|b|$≥$|a + b|$(用“$＞$”“$＜$”“$=$”“$\geqslant$”或“$\leqslant$”填空)。
【应用】(3) 利用上面得到的结论解决下面问题：
若 $|m|+|n| = 16$,$|m + n| = 2$,则 $m = $±9或±7。
【拓展】(4) 当 $a$,$b$,$c$ 满足什么条件时,$|a|+|b|+|c|＞|a + b + c|$？当a,b,c中有1个正数,2个负数或2个正数,1个负数或1个0,1个正数,1个负数时,|a|+|b|+|c|＞|a+b+c|.

答案： 【尝试】
(1)①＞ ②＞ ③= ④=；【归纳】
(2)≥；【应用】
(3)±9或±7；【拓展】
(4)当a,b,c中有1个正数,2个负数或2个正数,1个负数或1个0,1个正数,1个负数时,|a|+|b|+|c|＞|a+b+c|.