《2025年三维数字课堂七年级数学上册人教版》

1.【教材P116例3变式】下列变形符合等式的性质的是 (D)
A.若$3x - 5 = x + 2$,则$3x = x - 3$
B.若$-3x = 5$,则$x = 8$
C.若$5x = 7$,则$x = \frac{5}{7}$
D.若$-\frac{1}{4}x + 1 = 0.5$,则$\frac{1}{4}x = \frac{1}{2}$

答案： D

2. 把等式$m - 2n = n - 2m变形为m + 2m = n + 2n$是根据 (C)
A.在等式左右两端同时加$2m$,结果仍相等
B.在等式左右两端同时加$2n$,结果仍相等
C.在等式左右两端同时加$2m + 2n$,结果仍相等
D.在等式左右两端同时加$2m - 2n$,结果仍相等

答案： C

3. 下列等式变形正确的是 (B)
A.由$-3x = -3y$,得$x = -y$
B.由$a = b$,得$\frac{a}{-3} = \frac{b}{-3}$
C.由$\frac{x}{4} = 1$,得$x = \frac{1}{4}$
D.由$x = y$,得$\frac{x}{a} = \frac{y}{a}$

答案： B

4. 下列说法：
①在等式$2x = 4两边都加2$,可得等式$4x = 6$；
②在等式$2x = 4两边都减2$,可得等式$x = 2$；
③在等式$2x = 4两边都乘\frac{1}{2}$,等式变为$x = 4$；
④在等式$2x = 4两边都除以2$,可得等式$x = 2$。
其中正确的有 (A)
A.1个
B.2个
C.3个
D.4个

答案： A

5.【教材P116例3变式】若$4x - 7 = -21$,则可得$4x = -21 + \underline{7}$,这是根据等式的性质 1,在等式的左右两边 同时加7。

答案： 7 1 同时加7

6. 如果$4(x - \frac{2}{3}) = 2$,那么$x - \frac{2}{3} = \underline{\hspace{2cm}}$$\frac{1}{2}$

答案： $\frac{1}{2}$ 点拨:根据等式的性质2可得$x-\frac{2}{3}=$$\frac{2}{4}=\frac{1}{2}$.

7.【教材P116例4变式】利用等式的基本性质解下列方程并检验：
(1)$\frac{1}{3}x - \frac{1}{2} = -\frac{1}{6}$；
(2)$x + 20 = 6$.

答案： 解:
(1)两边都加$\frac{1}{2}$,得$\frac{1}{3}x-\frac{1}{2}+\frac{1}{2}=$$-\frac{1}{6}+\frac{1}{2}$.化简,得$\frac{1}{3}x=\frac{1}{3}$.两边同乘3,得$x=1$.检验,将$x=1$代入原方程的左边,得$\frac{1}{3}×$$1-\frac{1}{2}=-\frac{1}{6}$,方程的左右两边相等,所以$x=1$是原方程的解.
(2)两边都减去20,得$x+20-20=6-20$.化简,得$x=-14$.检验,把$x=-14$代入原方程的左边,得$-14+20=6$,方程的左右两边相等.所以$x=-14$是原方程的解.点拨:通过这两道题可知,利用等式的性质把方程变形为$x=a$($a$为常数)的形式,从而求得方程的解,而检验方程的解是根据方程的解的意义,把所求的值代入原方程的两边,看使方程的左右两边是否相等.

1. 如图5-1-2所示,两个天平都平衡,则与2个球的质量相等的正方体的个数为 (A)

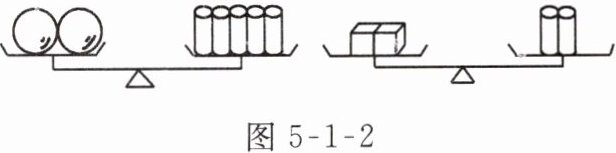
A.5个
B.4个
C.3个
D.2个

答案： A

2. 方程$3x + 6 = 0$的解的相反数是 (A)
A.2
B.-2
C.3
D.-3

答案： A

3. 用“●”“■”“▲”分别表示三种不同的物体,如图5-1-3所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“？”处应放“■”的个数为 (A)

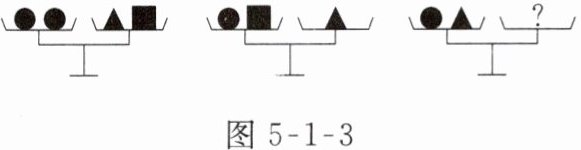
A.5个
B.4个
C.3个
D.2个

答案： A

4. 如果在等式$5(x + 2) = 2(x + 2)$的两边同除以$x + 2$就会得到$5 = 2$。我们知道$5 \neq 2$,由此可以猜测$x + 2$等于0。

答案： 0