第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1.【教材P44例4变式】计算$6÷(-3)$的结果是 (
A.$-\frac{1}{2}$
B.$-2$
C.$-3$
D.$-8$
B
)A.$-\frac{1}{2}$
B.$-2$
C.$-3$
D.$-8$
答案:
B
2.【教材P44例5变式】分数$\frac{-42}{-6}$可以化简为 (
A.$7$
B.$-7$
C.$6$
D.$-6$
A
)A.$7$
B.$-7$
C.$6$
D.$-6$
答案:
A
3.计算$1÷(-5)×(-\frac{1}{5})$的结果是 (
A.$1$
B.$-1$
C.$\frac{1}{25}$
D.$-\frac{1}{25}$
C
)A.$1$
B.$-1$
C.$\frac{1}{25}$
D.$-\frac{1}{25}$
答案:
C 点拨:乘、除是同一级运算,按照从左到右的顺序进行,所以原式$=1×\left(-\frac{1}{5}\right)×\left(-\frac{1}{5}\right)=\frac{1}{25}$.
4.计算$(-\frac{4}{7})÷(-\frac{3}{14})÷(-\frac{2}{3})$的结果是(
A.$-\frac{16}{9}$
B.$-4$
C.$4$
D.$-\frac{4}{49}$
B
)A.$-\frac{16}{9}$
B.$-4$
C.$4$
D.$-\frac{4}{49}$
答案:
B 点拨:把除法运算变为乘法运算,并确定出结果的符号,原式可变为$-\frac{4}{7}×\frac{14}{3}×\frac{3}{2}=-4$,故选B.
5.计算:
(1)$0.08÷(-0.4)$;
(2)$\frac{3}{5}÷(-3)$;
(3)$(-\frac{7}{9})÷(+3\frac{1}{2})$;
(4)$(-3)÷6×(-5)$;
(5)$-6×(-12)÷(-9)$;
(6)$(-5)÷(-1\frac{2}{7})×0×(-2\frac{1}{4})÷7$.
(1)$0.08÷(-0.4)$;
(2)$\frac{3}{5}÷(-3)$;
(3)$(-\frac{7}{9})÷(+3\frac{1}{2})$;
(4)$(-3)÷6×(-5)$;
(5)$-6×(-12)÷(-9)$;
(6)$(-5)÷(-1\frac{2}{7})×0×(-2\frac{1}{4})÷7$.
答案:
(1)-0.2
(2)$-\frac{1}{5}$
(3)$-\frac{2}{9}$
(4)$\frac{5}{2}$
(5)-8
(6)0
(1)-0.2
(2)$-\frac{1}{5}$
(3)$-\frac{2}{9}$
(4)$\frac{5}{2}$
(5)-8
(6)0
1.如果$\frac{|a|}{a}= -1$,那么$a$是 (
A.正数
B.负数
C.非负数
D.非正数
B
)A.正数
B.负数
C.非负数
D.非正数
答案:
B
2.有理数$|-1|,-(-1),-\frac{1}{-1},-\frac{-1}{-1}$中,化简的结果等于$1$的有 (
A.$1$个
B.$2$个
C.$3$个
D.$4$个
C
)A.$1$个
B.$2$个
C.$3$个
D.$4$个
答案:
C
3.【数形结合思想】有理数$a,b$在数轴上的位置如图2-2-5所示,则下列结论正确的是(
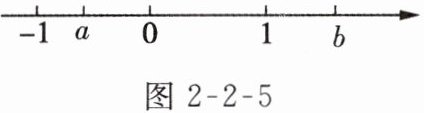
A.$a + b>0$
B.$a - b>0$
C.$ab>0$
D.$\frac{a}{b}>0$
A
)
A.$a + b>0$
B.$a - b>0$
C.$ab>0$
D.$\frac{a}{b}>0$
答案:
3.A 点拨:由图可知$-1< a<0$,$b>1$,所以$a+b>0$,$a-b<0$,$ab<0$,$\frac{a}{b}<0$.故选A.
查看更多完整答案,请扫码查看


