《2025年三维数字课堂七年级数学上册人教版》

4. 在一组连续整数$99$,$100$,$101$,$102$,…,$2024$前任意添加“$+$”号和“$-$”号,并运算,则可以得到的最小非负整数是(A)
A.$1$
B.$0$
C.$199$
D.$99$

答案： A 点拨：由题知，99-100-101+102=0，103-104-105+106=0，…，所以从99开始，在连续四个整数之间添加“+”号和“-”号可使其运算结果为0. 又因为2024-99+1=1926，即这组数据的个数为1926个，而1926÷4=481……2，所以这组数据前面的1924个数可使其运算结果为0，而最终余下的数为2023和2024，当添加符号运算为-2023+2024=1时，所得的结果为最小非负整数. 故选 A.

5. 【定义新运算】数学活动中,王老师给同学们出了一道题：规定一种新运算“★”,对于任意有理数$a和b$,有$a★b = a - b + 1$。请根据新运算,计算$(2★3)★2$的值是(B)
A.$0$
B.$-1$
C.$-2$
D.$1$

答案： B

6. 【跨学科融合—计算机】分别输入$-1$,$-2$,按如图 $2 - 1 - 2$ 所示的程序运算,则输出的结果依次是1,0。

答案： 1 0

7. 已知$\vert x\vert = 2$,$\vert y\vert = 3$,$\vert z\vert = 5$,且$x ＞ y ＞ z$,则$3x - 4y - 2z$的值是28或16。

答案： 28或16 点拨：由|x|=2，|y|=3，|z|=5，可知x=±2，y=±3，z=±5. 又x＞y＞z，所以x=2，y=-3，z=-5或x=-2，y=-3，z=-5. 所以3x-4y-2z=28或16.

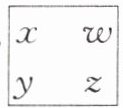
8. 【定义新运算】若“方框”$\begin{array}{cc}x&w\\y&z\end{array} 表示运算x - y + z + w$,则“方框”$\begin{array}{cc}-2&3\\3&-6\end{array} = $-8。

答案： -8

9. 【实际应用问题】在一条铁路建设项目中要测量$B$地高度,但不易测量,现知道$A地高度为6.3m$,我们在$A$,$B两地间找到合适的四个中间地点D$,$E$,$F$,$G$,每次测量结果如下表(单位：$m$)：
| $D比A$低 | $E比D$低 | $F比E$低 | $G比F$低 | $B比G$低 |
| :---: | :---: | :---: | :---: | :---: |
| $3.6$ | $-5.2$ | $-0.8$ | $4.4$ | $-5.9$ |

$B$地高度是多少米？

答案： 6.3-3.6-(-5.2)-(-0.8)-4.4-(-5.9)=10.2(m)

1. 【阅读理解问题】观察下列等式：
$①\frac{1}{2} - 1 = -\frac{1}{2}；$$②\frac{1}{3} - \frac{1}{2} = -\frac{1}{6}；$$③\frac{1}{4} - \frac{1}{3} = -\frac{1}{12}；$…(1) 依照上述规律,请写出第④和第⑤个等式。(2) 计算：$-\frac{1}{2} - \frac{1}{6} - \frac{1}{12} - … - \frac{1}{90}。$

答案：
(1)第④个等式为$\frac{1}{5}-\frac{1}{4}=-\frac{1}{20}$；第⑤个等式为$\frac{1}{6}-\frac{1}{5}=-\frac{1}{30}$.
(2)原式=$(\frac{1}{2}-1)+(\frac{1}{3}-\frac{1}{2})+(\frac{1}{4}-\frac{1}{3})+\cdots+(\frac{1}{10}-\frac{1}{9})=-1+\frac{1}{10}=-\frac{9}{10}$

2. 【计算机应用问题】电子跳蚤落在数轴上的某点,第$1步从K_0向左跳1个单位长度到K_1$,第$2步从K_1向右跳2个单位长度到K_2$,第$3步从K_2向左跳3个单位长度到K_3$,第$4步由K_3向右跳4个单位长度到K_4$,…$$,按以上规律跳到第$100$步时,电子跳蚤落在数轴上的$K_{100}$处,且所表示的数恰好是$19.94$,试求电子跳蚤的初始位置$K_0$所表示的数。

答案： 解：设初始位置$K_0$所表示的数为x，向左跳记为负，向右跳记为正，则$K_1$，$K_2$，…，$K_{100}$所表示的有理数分别为x-1，x-1+2，x-1+2-3，…，x-1+2-3+…-99+100，于是x-1+2-3+…-99+100=19.94，从而x=-30.06.