《2025年三维数字课堂七年级数学上册人教版》

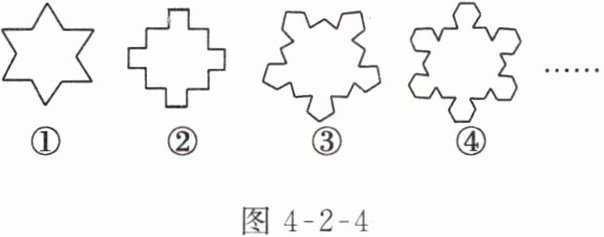
6.如图4-2-4所示,①中多边形(边数为$12$)是由正三角形“扩展”而来的,②中多边形是由正方形“扩展”而来的,…$$,以此类推,则由正$n$边形“扩展”而来的多边形的边数为$n^{2}+n$.

答案： $n^{2}+n$

7.【教材P100例7变式】某工厂第一车间有$a$人,第二车间比第一车间的人数少$30$人.
(1)两个车间共有多少人?
(2)如果从第二车间调出$10$人到第一车间,那么调动后,第一车间的人数比第二车间多多少人?

答案： 解:
(1)$a+a-30=(2a-30)$(人).
(2)$a+10-(a-30-10)=50$(人).

1.【阅读理解问题】阅读材料：
我们知道,$4x - 2x + x= (4 - 2 + 1)x = 3x$.类似地,我们把$a + b$看成一个整体,则$4(a + b)-2(a + b)+(a + b)= (4 - 2 + 1)(a + b)= 3(a + b)$.“整体思想”是中学数学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用：
(1)若把$(a - b)^{2}$看成一个整体,则合并$3(a - b)^{2}-6(a - b)^{2}+2(a - b)^{2}$的结果是$-(a-b)^{2}$.
(2)若$x^{2}-2y = 5$,求$3x^{2}-6y - 23$的值.
(3)若$a - 2b = 3,2b - c = - 4,c - d = 10$,若$(a - c)+(2b - d)-(2b - c)$的值.

答案： 解:
(1)$-(a-b)^{2}$
(2)$\because x^{2}-2y=5,$
∴原式$=3(x^{2}-2y)-23=3×5-23=15-23=-8.$
(3)$\because a-2b=3$①,$2b-c=-4$②,$c-d=10③,$
∴①+②,得$a-c=-1;$②+③,得$2b-d=6.$$\therefore (a-c)+(2b-d)-(2b-c)=-1+6-(-4)=9.$

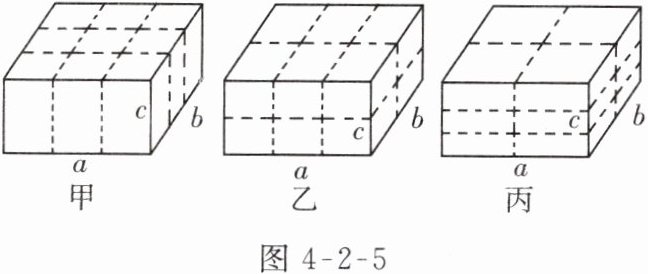
2.【实际应用问题】有一长方体形状的物体,它的长、宽、高分别为$a$、$b$、$c(a＞b＞c)$,有三种不同的捆扎方式(如图4-2-5所示的虚线),哪种方式用绳最少?哪种方式用绳最多?说明理由.

答案： 解:甲种方式所用绳长为$4a+4b+8c$,乙种方式所用绳长为$4a+6b+6c$,丙种方式所用绳长为$6a+6b+4c$,因为$a＞b＞c$,所以乙种方式比甲种方式多用绳$(4a+6b+6c)-(4a+4b+8c)=2b-2c$,丙种方式比乙种方式多用绳$(6a+6b+4c)-(4a+6b+6c)=2a-2c$.因此,甲种方式用绳最少,丙种方式用绳最多.点拨:用整式的加减来揭示一般性规律,体现了数学知识在实际生活中的应用.