《2025年三维数字课堂七年级数学上册人教版》

1. 【教材 P114 例 2 变式】以 $ x = - 2 $ 为解的方程是(C)
A.$ - 2x + 5 = 3x + 10 $
B.$ x ^ { 2 } - 4 = 4x $
C.$ x ( x - 2 ) = - 4x $
D.$ 5x - 3 = 6x - 2 $

答案： C 点拨:把x=-2代入方程逐一进行检验,看能否使方程中等号左右两边的值相等.

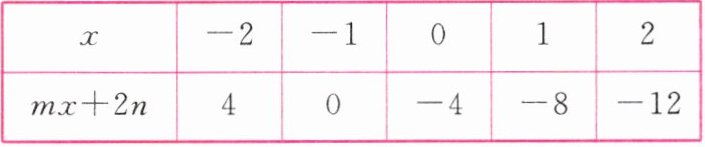
2. 整式 $ mx + 2n $ 的值随 $ x $ 的取值不同而不同,下表是当 $ x $ 取不同值时对应的整式值,则关于 $ x $ 的方程 $ \frac { 1 } { 2 } mx + n = 2 $ 的解为(A)
| $ x $ | $ - 2 $ | $ - 1 $ | $ 0 $ | $ 1 $ | $ 2 $ |
| $ mx + 2n $ | $ 4 $ | $ 0 $ | $ - 4 $ | $ - 8 $ | $ - 12 $ |

A.$ x = - 2 $
B.$ x = - 1 $
C.$ x = 0 $
D.$ x = 2 $

答案： A 点拨:因为当x=-2时,mx+2n=4,所以当x=-2时,$\frac{1}{2}mx+n=2$,故选A.

3. 在方程：① $ \frac { 1 } { 3 } x = 1 $；② $ 2x - 3 = 1 $；③ $ \frac { 2 } { 3 } x - \frac { 3 } { 2 } = \frac { 3 } { 7 } $；④ $ ( x + 1 ) ( x + 2 ) = 12 $；⑤ $ 2x - \frac { 2 } { x } = 3 $；⑥ $ 2 [ 3x - ( x - 3 ) ] - 3 = 11 $ 中,$ x = 2 $ 是其解的方程有②④⑤⑥(填序号)。

答案： ②④⑤⑥ 点拨:将x=2代入验证.

4. 【教材 P115 练习 2 变式】下列各式中,哪些是方程？哪些是一元一次方程？
(1)$ \frac { x } { 5 } - 1 = 3 $；
(2)$ 2x - 1 $；
(3)$ \frac { 1 } { 2 } x + 1 = \frac { 1 } { 2 } x - 1 $；
(4)$ 5 + 2 = 7 $；
(5)$ 3x - 1 = - x ^ { 2 } $。

答案： 解:
(1)
(5)是方程;
(1)是一元一次方程. 点拨:判断一个式子是不是方程,首先看它是不是等式,再看它经过整理后是否含未知数,如果是方程,且只含一个未知数,未知数的次数是1,那么它就是一元一次方程.

1. 已知下列式子：
① $ 23 - x $；② $ 2a - b = 3 $；③ $ y + 3 = 6y - 9 $；
④ $ x - 2 = \frac { 2 } { x } $；⑤ $ x ^ { 2 } = 1 $；⑥ $ \frac { 1 } { 2 } y - 4 = \frac { 1 } { 3 } y $。
其中是一元一次方程的有(A)
A.$ 2 $ 个
B.$ 3 $ 个
C.$ 4 $ 个
D.$ 5 $ 个

答案： A 点拨:①不是,因为不是等式;②不是,因为含有两个未知数;③是一元一次方程;④不是,因为分母中含有未知数;⑤不是,因为未知数的次数不是1;⑥是一元一次方程.故选A.

2. 若 $ ( 2 - a ) x ^ { 2b - 3 } - 5 = 0 $ 是关于 $ x $ 的一元一次方程,则 $ a \neq $2,$ b = $2。

答案： 2 2 点拨:一元一次方程的未知数次数是1,即2b-3=1,b=2;若有未知数存在,则必须2-a≠0,即a≠2.

3. 某市在端午节准备举行划龙舟大赛,预计 $ 15 $ 个队共 $ 330 $ 人参加。已知每个队一条船,每条船上人数相等,且每条船上有 $ 1 $ 人击鼓,$ 1 $ 人掌舵,其余的人同时划桨。如果设每条船上划桨的有 $ x $ 人,那么可列出的方程为15(x+1+1)=330。

答案： 15(x+1+1)=330

4. 爸爸与儿子下象棋,爸爸赢 $ 1 $ 盘记 $ 1 $ 分,儿子赢 $ 1 $ 盘记 $ 3 $ 分,下了 $ 8 $ 盘后,两人得分相等,那么他们各赢了多少盘？对于这个问题,请设未知数并列出方程。

答案： 解:设爸爸赢了x盘,则可列方程为x=3(8-x).