《2025年三维数字课堂七年级数学上册人教版》

8. 已知 $ \frac { 2 } { 1 } × 2 = \frac { 2 } { 1 } + 2 $,$ \frac { 3 } { 2 } × 3 = \frac { 3 } { 2 } + 3 $,$ \frac { 4 } { 3 } × 4 = \frac { 4 } { 3 } + 4 $,…,若 $ \frac { a } { b } × 10 = \frac { a } { b } + 10 $($ a $,$ b $ 都是正整数),则 $ a + b $ 的值是 19.

答案： 19

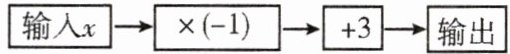
9. $ \boxed{输入x} \rightarrow \boxed{× (-1)} \rightarrow \boxed{+3} \rightarrow \boxed{输出} $ 是一个简单的数值运算流程图,当输入 $ x = - 1 $ 时,输出的数值为 4.

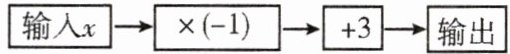
答案： 4

10. 【实际应用问题】星期天,小明和小华两人利用温度差测量山峰的高度,小明在山顶测得温度是 $ - 2 ^ { \circ } \mathrm { C } $,小华在山脚测得温度是 $ 5 ^ { \circ } \mathrm { C } $.已知该山区高度每上升 $ 100 \mathrm { m } $,气温大约降低 $ 0.7 ^ { \circ } \mathrm { C } $,那么这个山峰的高度大约是多少米？

答案： 解:$100×\{[5-(-2)]÷0.7\}=1000(m)$，所以这个山峰的高度大约是 1000m.

11. 【阅读理解问题】先阅读下面的材料,再回答后面的问题.
计算：$ 10 ÷ ( \frac { 1 } { 2 } - \frac { 1 } { 3 } + \frac { 1 } { 6 } ) $.
解法一：原式 $ = 10 ÷ ( \frac { 3 } { 6 } - \frac { 2 } { 6 } + \frac { 1 } { 6 } ) = 10 ÷ \frac { 2 } { 6 } = 10 × 3 = 30 $.
解法二：原式的倒数为：$ ( \frac { 1 } { 2 } - \frac { 1 } { 3 } + \frac { 1 } { 6 } ) ÷ 10 = ( \frac { 1 } { 2 } - \frac { 1 } { 3 } + \frac { 1 } { 6 } ) × \frac { 1 } { 10 } = \frac { 1 } { 2 } × \frac { 1 } { 10 } - \frac { 1 } { 3 } × \frac { 1 } { 10 } + \frac { 1 } { 6 } × \frac { 1 } { 10 } = \frac { 1 } { 30 } $.
故原式 $ = 30 $.
请选择上述的一种解法解决下面的问题.
计算：$ ( - \frac { 1 } { 28 } ) ÷ ( \frac { 1 } { 2 } - \frac { 1 } { 4 } + \frac { 1 } { 7 } - \frac { 1 } { 14 } ) $.
解:解法一:原式$=(-\frac{1}{28})÷(\frac{14}{28}-\frac{7}{28}+\frac{4}{28}-\frac{2}{28})=(-\frac{1}{28})÷\frac{9}{28}=(-\frac{1}{28})×\frac{28}{9}=-\frac{1}{9}$.解法二:原式的倒数为:$(\frac{1}{2}-\frac{1}{4}+\frac{1}{7}-\frac{1}{14})÷(-\frac{1}{28})=(\frac{1}{2}-\frac{1}{4}+\frac{1}{7}-\frac{1}{14})×(-28)=\frac{1}{2}×(-28)-\frac{1}{4}×(-28)+\frac{1}{7}×(-28)-\frac{1}{14}×(-28)=-14+7-4+2=-9$.故原式$=-\frac{1}{9}$.

答案： 解:解法一:原式$=(-\frac{1}{28})÷(\frac{14}{28}-\frac{7}{28}+$$\frac{4}{28}-\frac{2}{28})=(-\frac{1}{28})÷\frac{9}{28}=(-\frac{1}{28})×\frac{28}{9}=$$-\frac{1}{9}$.解法二:原式的倒数为:$(\frac{1}{2}-\frac{1}{4}+\frac{1}{7}-\frac{1}{14})÷$$(-\frac{1}{28})=(\frac{1}{2}-\frac{1}{4}+\frac{1}{7}-\frac{1}{14})×(-28)=$$\frac{1}{2}×(-28)-\frac{1}{4}×(-28)+\frac{1}{7}×(-28)-$$\frac{1}{14}×(-28)=-14+7-4+2=-9$.故原式$=-\frac{1}{9}$.

1. 【推理问题】小丽有 5 张写着不同数字的卡片(如图 2 - 2 - 6 所示),请按要求抽出卡片,解答下列各问题：
(1) 从中抽出 3 张卡片,如何抽取才能使这 3 张卡片上的数字先让两个数相乘再与第三个数相除的结果最大？最大结果是多少？
(2) 从中抽出 3 张卡片,如何抽取才能使这 3 张卡片上的数字先让两个数相乘再与第三个数相除的结果最小？最小结果多少？

答案： 解:
(1)抽取-5，-3，$+\frac{1}{4}$，最大结果为$(-5)×(-3)÷\frac{1}{4}=60$.
(2)抽取-5，+3，$+\frac{1}{4}$，最小结果为$(-5)×3÷\frac{1}{4}=-60$.

2. 【实际应用问题】某商场在“十一”期间举办优惠促销活动,采取“满 100 元送 20 元,并且连环赠送”的酬宾方式,即顾客每消费 100 元(这里的 100 元可以是现金,也可以是奖励券,还可以是两者合计的钱数)就送 20 元奖励券,满 200 元就送 40 元奖励券,以此类推.在此期间,一位顾客一次性购物花了 20000 元.那么他可以多买多少钱的商品？此次购物相当于打了几折？

答案： 解:因为$20000×\frac{20}{100}=4000(元)$，所以买 20000 元的商品可得到 4000 元奖励券.因为$4000×\frac{20}{100}=800(元)$，所以买 4000 元的商品可得到 800 元奖励券.因为$800×\frac{20}{100}=160(元)$，所以买 800 元的商品可得到 160 元奖励券.又因为买 100 元的商品可得到 20 元奖励券，所以共得奖励券$4000+800+160+20=4980(元)$.故可以多买 4980 元的商品.$20000÷(20000+4980)\approx80\%$.所以此次购物相当于打了八折.点拨：此顾客一次性购买了 20000 元的商品，可得奖励券$20000×\frac{20}{100}=4000(元)$，再用这 4000 元奖励券购物，又可得奖励券$4000×\frac{20}{100}=800(元)$，用 800 元去购物，又可得奖励券$800×\frac{20}{100}=160(元)$，因为只有满 100 元才赠送 20 元奖励券，所以在 160 元中拿出 100 元购物，可得到 20 元奖励券，加上剩余的 60 元，还可购买 80 元的商品.所以这位顾客在此次购物中共得奖励券$4000+800+160+20=4980(元)$.他可以多买 4980 元的商品.经计算可知，此次购物相当于打了八折.