《2025年同步练习册大象出版社七年级数学上册人教版》

13. (★)把下列各数填入相应的集合内：
$ +8.5,-3\frac{1}{2},0.3,0,-3.4,12,-9,4\frac{1}{3},-1.2,-2 $
(1) 正有理数集合：{
...}；
(2) 整数集合：{
...}；
(3) 自然数集合：{
...}；
(4) 负分数集合：{
...}。

答案：
(1)正有理数集合:$\left\{ +8.5,0,3,12,4\frac{1}{3},\cdots \right\}$
(2)整数集合:$\{ 0,12,-9,-2,\cdots \}$
(3)自然数集合:$\{ 0,12,\cdots \}$
(4)负分数集合:$\left\{ -3\frac{1}{2},-3.4,-1.2,\cdots \right\}$

14. (★)有以下几组数：①$ \frac{1}{2} $ 与 $ -0.5 $；②$ -(+3) $ 与 $ +(-3) $；③$ -(-6) $ 与 $ +(-6) $；④$ -(-4) $ 与 $ +(+4) $。其中互为相反数的有 【B】
A.1 组
B.2 组
C.3 组
D.4 组

答案： B

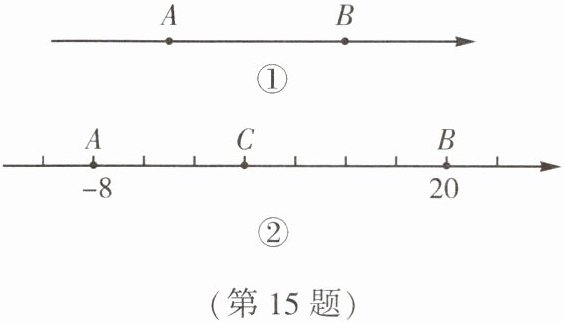
15. (★★)数学课上,李老师说：咱们一起来玩一个找原点的游戏吧！
(1) 如图①,数轴上标有 $ A,B $ 两点,已知 $ A,B $ 两点所表示的数互为相反数。
①如果点 $ A $ 表示的数是 $ -5 $,那么点 $ B $ 表示的数是______；
②在图①中标出原点 $ O $ 的位置。
(2) 图②是小慧所画的数轴,数轴上标出的刻度中任意相邻两刻度间的距离都相等。根据小慧提供的信息,标出隐藏的原点 $ O $ 的位置,写出此时点 $ C $ 表示的数：______。

答案：

(1)①5 ②原点 O 的位置如图所示.
(2)原点 O 的位置如图所示. 4

16. (★)有理数 $ a,b $ 在数轴上的对应点的位置如图所示,则 $ a,b,-a,|b| $ 的大小关系正确的是 【B】

A.$ |b|＞a＞-a＞b $
B.$ |b|＞b＞a＞-a $
C.$ a＞|b|＞b＞-a $
D.$ a＞|b|＞-a＞b $

答案： B

17. (★)比较大小：(1) $ -\frac{2}{3} $＞$ -\frac{3}{4} $；(2) $ -(-5) $＞$ -|-5| $。

答案：
(1)$＞$
(2)$＞$

18. (★★)数轴是展现数形结合思想的一个重要工具。有了数轴以后,可以用数轴上的点直观地表示有理数,这样就建立起了“数”与“形”之间的联系。同时,数轴也是我们研究相反数、绝对值的直观工具。如图,数轴上有 $ A,B,C,D $ 四个点。

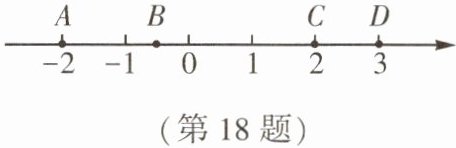
(1)$ A,B,C,D $ 所对应的数的绝对值最小的是 【B】
A. 点 $ A $ B. 点 $ B $
C. 点 $ C $ D. 点 $ D $
(2) 点 $ A $ 与点 $ D $ 间的距离为5。

答案：
(1)B
(2)5