《2025年启东中学作业本九年级数学上册苏科版徐州专版》

9. 如图,在四边形$ABDC$中,$AB = AC = 3$,$BD = CD = 2$,将它以$AD所在直线为轴旋转180^{\circ}$后,得到的以$AB$,$BD$为母线的上、下两个圆锥的侧面积之比为3:2.

答案： 3:2

10. 如图,在$□ ABCD$中,$AB= \sqrt{3}+1$,$BC = 2$,$AH\perp CD$,垂足为$H$,$AH= \sqrt{3}$. 以点$A$为圆心,$AH$为半径画弧,与$AB$,$AC$,$AD分别交于点E$,$F$,$G$. 若用扇形$AEF$围成一个圆锥的侧面,记这个圆锥底面圆的半径为$r_{1}$；用扇形$AHG$围成另一个圆锥的侧面,记这个圆锥底面圆的半径为$r_{2}$,则$r_{1}-r_{2}= $$\frac{\sqrt{3}}{24}$.(结果保留根号)

答案： $\frac{\sqrt{3}}{24}$

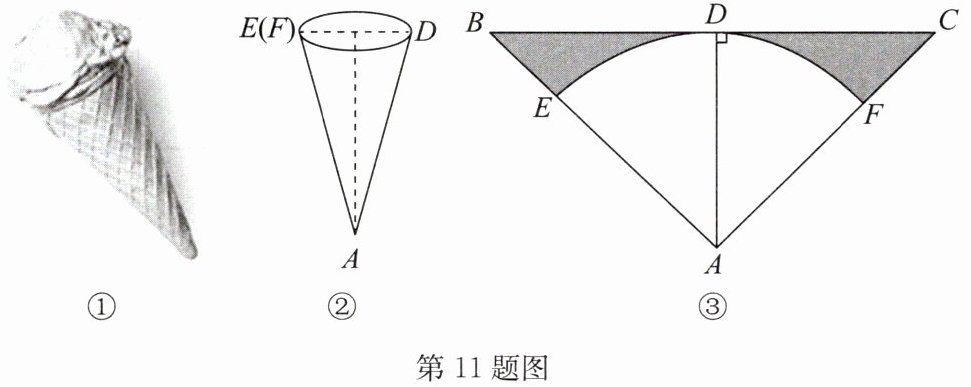
11. 如图①,某种冰激凌的外包装可以视为圆锥,如图②,它的底面圆直径$ED与母线AD长之比为1:2$. 制作这种外包装需要用如图③所示的等腰三角形材料,其中$AB = AC$,$AD\perp BC$. 将扇形$AEF$围成圆锥时,$AE$,$AF$恰好重合.
(1)求这种加工材料的顶角$\angle BAC$的大小；
(2)若圆锥的底面圆直径$ED$为5 cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留$\pi$)

答案： 解:
(1)设∠BAC=n°.
根据题意,得$\pi\cdot DE=\frac{n\pi\cdot AD}{180}$.
∵AD=2DE,
∴n=90.
答:这种加工材料的顶角∠BAC为90°.
(2)
∵AD=2DE=10cm,
∴$S_{阴影}=\frac{1}{2}BC\cdot AD-S_{扇形AEF}=\frac{1}{2}$×20×10−$\frac{90\pi×10^{2}}{360}$=(100−25π)cm².
答:加工材料剩余部分的面积为(100−25π)cm².

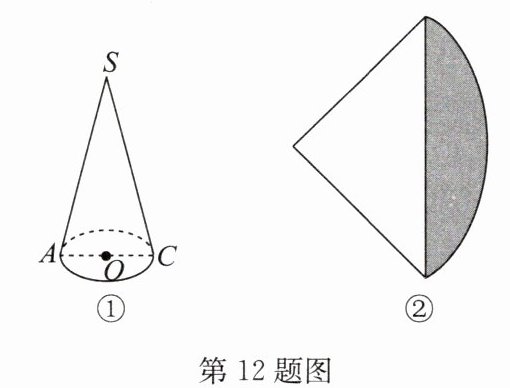
12. 如图①,圆锥底面圆的半径为1,母线长为4,图②为其侧面展开图.
(1)求阴影部分的面积；(结果保留$\pi$)
(2)母线$SC$是一条蜜糖线,一只蚂蚁从点$A$沿着圆锥表面最少需要爬多远才能吃到蜜糖?

答案：
解:
(1)如答图,作SE⊥AF交$\overset{\frown}{AF}$于点C.
设答图中的扇形的圆心角为n°,
根据题意，得$\frac{n\pi×4}{180}=2\pi×1$,解得$n=90$.
∵SA=SF,
∴△SFA是等腰直角三角形,
∴AF=4√2,
∴SE=$\frac{1}{2}$AF=$\frac{1}{2}$×4$\sqrt{2}$=2$\sqrt{2}$,
∴$S_{阴影}=S_{扇形SAF}-S_{\triangle SAF}=\frac{90\pi×4^{2}}{360}-\frac{1}{2}$×4$\sqrt{2}$×2$\sqrt{2}$=4π−8.

(2)
∵SC是一条蜜糖线,AE⊥SC,AE=2$\sqrt{2}$,
∴根据垂线段最短,一只蚂蚁从点A沿着圆锥表面最少需要爬$2\sqrt{2}$个单位长度才能吃到蜜糖.