《2025年启东中学作业本九年级数学上册苏科版徐州专版》

1. (2024·无锡)已知圆锥的底面圆半径为3,母线长为4,则圆锥的侧面积为 (B)
A.$6\pi$
B.$12\pi$
C.$15\pi$
D.$24\pi$

答案： B

2. (2024·姑苏区二模)若圆锥的侧面展开图是圆心角为$120^{\circ}$的扇形,则该圆锥的侧面积与底面积的比为 (C)
A.$3:2$
B.$2:1$
C.$3:1$
D.$4:1$

答案： C

3. 如图,若圆锥的母线长为6,底面圆半径为2,则其侧面展开图圆心角的度数为120°.

答案： 120°

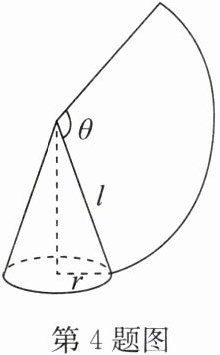
4. (2024·宿迁期末)如图,用半径为15、圆心角为$120^{\circ}$的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆的半径为5.

答案： 5

5. 如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 1$,$BC= \sqrt{3}$. 若把$\triangle ABC绕边AB$所在的直线旋转一周,则所得几何体的全面积为$\frac{\sqrt{3}+3}{2}\pi$.

答案： $\frac{\sqrt{3}+3}{2}\pi$

6. 如图,将弧长为$6\pi$,圆心角为$120^{\circ}的扇形纸片OAB$围成圆锥形纸帽,使扇形的两条半径$OA与OB$重合(接缝粘连部分忽略不计),求圆锥的底面圆半径及圆锥的侧面积.

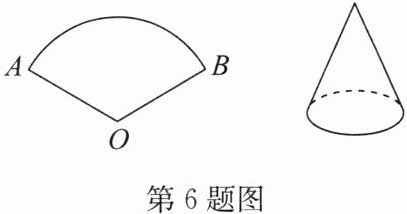
答案： 解:设圆锥的底面圆半径为r,则$2\pi r=6\pi$,解得$r=3$.
设扇形OAB的半径为R，根据题意，得$\frac{120}{180}$×π×R=6π,解得$R=9$.
∴圆锥的侧面积为$\frac{1}{2}$×6π×9=27π.

7. 如图,从一张腰长为90 cm,顶角为$120^{\circ}的等腰三角形铁皮OAB中剪出一个最大的扇形OCD$,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面圆半径为 (A)
A.15 cm
B.12 cm
C.10 cm
D.20 cm

答案： A

8. 如图,小珍同学用半径为8 cm,圆心角为$100^{\circ}$的扇形纸片,制作一个底面半径为2 cm的圆锥侧面,则圆锥上粘贴部分的面积是$\frac{16\pi}{9}$$cm^{2}$.

答案： $\frac{16\pi}{9}$