《2025年启东中学作业本九年级数学上册苏科版徐州专版》

9. 武侯区某学校开展了该校八年级部分学生的综合素质测评活动,随机选取了该校八年级的50名学生进行测评,统计数据如下表:

(1)求这50名学生的测评成绩的平均数、众数、中位数和方差;
(2)若该校八年级共有300名学生,测评成绩在90分以上(包含90分)为优秀,试估计该校八年级获得优秀的学生人数.

答案： 1. （1）
首先求平均数$\overline{x}$：
根据平均数公式$\overline{x}=\frac{x_{1}f_{1}+x_{2}f_{2}+\cdots +x_{n}f_{n}}{f_{1}+f_{2}+\cdots +f_{n}}$（其中$x_{i}$是数据，$f_{i}$是频数）。
这里$x_{1}=80$，$f_{1}=5$；$x_{2}=85$，$f_{2}=10$；$x_{3}=90$，$f_{3}=10$；$x_{4}=95$，$f_{4}=20$；$x_{5}=100$，$f_{5}=5$。
则$\overline{x}=\frac{80×5 + 85×10+90×10+95×20+100×5}{5 + 10+10+20+5}$
先计算分子：$80×5=400$，$85×10 = 850$，$90×10=900$，$95×20 = 1900$，$100×5=500$。
分子$=400 + 850+900+1900+500=4550$，分母$=50$。
所以$\overline{x}=\frac{4550}{50}=91$（分）。
然后求众数：
众数是一组数据中出现次数最多的数据。
因为$95$分出现的次数$20$次最多，所以众数是$95$分。
接着求中位数：
数据总数$n = 50$（$n$为偶数），中位数是按顺序排列的第$\frac{n}{2}$和$\frac{n}{2}+1$个数的平均数。
先将数据按从小到大顺序排列，$5$个$80$，$10$个$85$，$10$个$90$，$20$个$95$，$5$个$100$。
第$25$个数和第$26$个数都是$90$分，所以中位数$=\frac{90 + 90}{2}=90$（分）。
最后求方差$s^{2}$：
根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\overline{x})^{2}f_{1}+(x_{2}-\overline{x})^{2}f_{2}+\cdots+(x_{n}-\overline{x})^{2}f_{n}]$。
$n = 50$，$\overline{x}=91$，$(x_{1}-\overline{x})^{2}f_{1}=(80 - 91)^{2}×5=(-11)^{2}×5=121×5 = 605$；$(x_{2}-\overline{x})^{2}f_{2}=(85 - 91)^{2}×10=(-6)^{2}×10 = 36×10=360$；$(x_{3}-\overline{x})^{2}f_{3}=(90 - 91)^{2}×10=(-1)^{2}×10 = 10$；$(x_{4}-\overline{x})^{2}f_{4}=(95 - 91)^{2}×20=4^{2}×20=16×20 = 320$；$(x_{5}-\overline{x})^{2}f_{5}=(100 - 91)^{2}×5=9^{2}×5=405$。
$s^{2}=\frac{605+360 + 10+320+405}{50}=\frac{1700}{50}=34$。
2. （2）
先计算$50$名学生中优秀（$90$分以上（包含$90$分））的人数：$10 + 20+5=35$（人）。
设$300$名学生中优秀人数为$x$。
由比例关系$\frac{x}{300}=\frac{35}{50}$。
交叉相乘得$50x=300×35$。
则$x=\frac{300×35}{50}=210$（人）。
综上，（1）平均数是$91$分，众数是$95$分，中位数是$90$分，方差是$34$；（2）该校八年级获得优秀的学生人数约为$210$人。

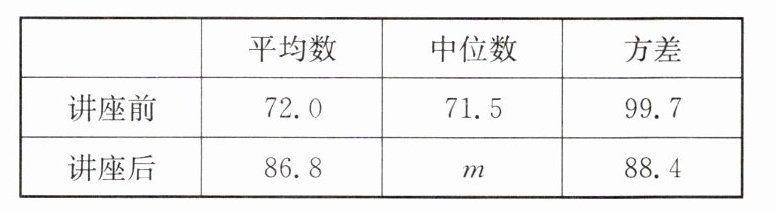
10. (2024·常州一模)某社区通过公益讲座的方式普及垃圾分类知识.为了了解居民对相关知识的了解情况及讲座效果,请居民在讲座前和讲座后分别回答了一份垃圾分类知识问卷,从中随机抽取20名居民的两次问卷成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.

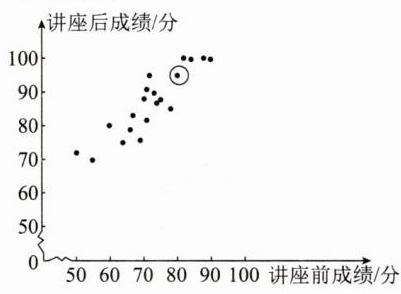
A. 这20名居民讲座前、讲座后成绩得分统计图如图所示;
B. 这20名居民讲座前、讲座后成绩的平均数、中位数、方差如下表;

C. 结合讲座后成绩x,被抽取的20名居民中有5人获得“参与奖”$(x＜80)$,有7人获得“优秀奖”$(80≤x＜90)$,有8人获得“环保达人奖”$(90≤x≤100)$,其中成绩在$80≤x＜90$这一组的是:80,82,83,85,87,88,88.
根据以上信息,回答下列问题:
(1)居民小张讲座前的成绩为80分,讲座后的成绩为95分,在图中圈出代表居民小张的点;
(2)写出表中m的值;
(3)若参加公益讲座的居民有160人,估计能获得“环保达人奖”的人数.

答案：

(1) （在图中讲座前成绩80分对应的点中，讲座后成绩为95分的点处圈出）

(2) 解：由C知讲座后成绩各区间人数：$x＜80$有5人，$80≤x＜90$有7人，$90≤x≤100$有8人，共20人。将讲座后成绩从小到大排列，第10、11个数在$80≤x＜90$组。该组数据为80,82,83,85,87,88,88，前两组共$5+7=12$人，第10个数是该组第5个数87，第11个数是该组第6个数88，中位数$m=\frac{87+88}{2}=87.5$
(3) 解：抽取的20人中“环保达人奖”占比为$\frac{8}{20}$，估计160人中人数为$160×\frac{8}{20}=64$人
答：
(2) $m=87.5$；
(3) 估计能获得“环保达人奖”的人数为64人。