《2025年启东中学作业本九年级数学上册苏科版徐州专版》

8.一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为$3:1$,则圆的面积约为正方形面积的(B)
A.27倍
B.14倍
C.9倍
D.3倍

答案： B

9.(南京期中)如图,两个正六边形的顶点A,B,C,D都在圆上.若$AB= 2$,则该圆的半径为$\sqrt{13}$.

答案： $\sqrt{13}$

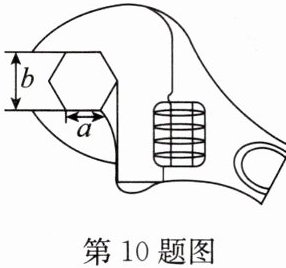
10.如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度$b= 3cm$,则螺帽边长$a= $$\sqrt{3}$cm.

答案： $\sqrt{3}$

11.如图,六边形ABCDEF是$\odot O$的内接正六边形,设正六边形ABCDEF的面积为$S_{1},△ACE的面积为S_{2}$,则$\frac {S_{1}}{S_{2}}= $2.

答案： 2

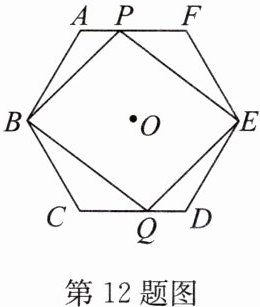
12.如图,中心为O的正六边形ABCDEF的半径为6cm,点P,Q同时分别从A,D两点出发,以1cm/s的速度沿AF,DC向终点F,C运动,连接PB,PE,QB,QE,设运动时间为$t(s).$
(1)求证:四边形PBQE为平行四边形;
(2)求矩形PBQE的面积与正六边形ABCDEF的面积之比.

答案：

(1)证明:
∵六边形ABCDEF是正六边形，
　
∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F.
　
∵点P,Q同时分别从A,D两点出发，以1cm/s的速度沿AF,DC向终点F,C运动，
　
∴AP=DQ=t,PF=QC=6−t.
　在△ABP和△DEQ中，{AB=DE,∠A=∠D,AP=DQ,
　
∴△ABP≌△DEQ(SAS),
∴BP=EQ,
　　同理可证PE=QB,
∴四边形PEQB为平行四边形.
(2)解:如答图①,连接BE,OA,则∠AOB=$\frac{360°}{6}$=60°.
∵OA=OB,
∴△AOB是等边三角形，
　
∴AB=OA=6,BE=2OB=12.
　　当t=0时，点P与点A重合，点Q与点D重合，四边形PBQE即为四边形ABDE，如答图①所示，
　　则∠EAF=∠AEF=30°,
　
∴∠BAE=∠BAF−∠FAE=120°−30°=90°,
　此时四边形ABDE是矩形，即四边形PBQE是矩形.
当t=6时,点P与点F重合,点Q与点C重合,四边形PBQE即为四边形FBCE,如答图②所示，
　同法可知∠BFE=90°,此时四边形PBQE是矩形.
　综上所述，当t=0s或6s时，四边形PBQE是矩形,则AE=$\sqrt{12²−6²}$=6$\sqrt{3}$,
∴矩形PBQE的面积=矩形ABDE的面积=AB×AE=6×6$\sqrt{3}$=36$\sqrt{3}$
∵正六边形ABCDEF的面积=6△AOB的面积=6×$\frac{1}{4}$矩形ABDE的面积=6×$\frac{1}{4}$×36$\sqrt{3}$=54$\sqrt{3}$,
∴矩形PBQE的面积与正六边形ABCDEF的面积之比为$\frac{2}{3}$.
　　　　

13.(1)如图①,$△ABC是\odot O$的内接正三角形,P为劣弧$\widehat {BC}$上一动点.求证:$PA= PB+PC;$
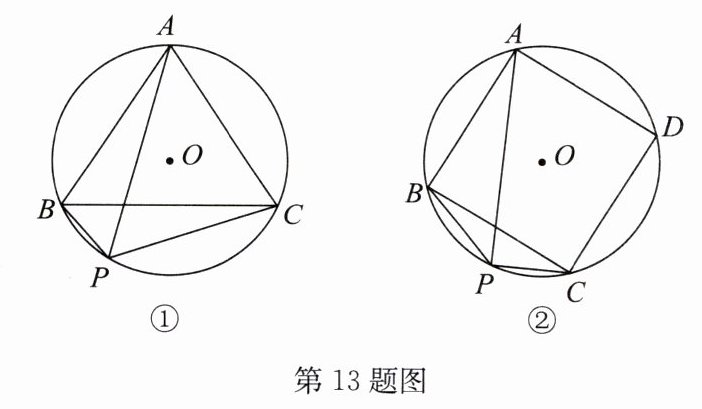
(2)如图②,四边形ABCD是$\odot O$的内接正方形,P为劣弧$\widehat {BC}$上一动点.求证:$PA= PC+\sqrt {2}PB.$

答案： $(1)$ 证明$PA = PB + PC$
解：延长$BP$至$E$，使$PE = PC$，连接$CE$。
因为$\triangle ABC$是正三角形，所以$\angle BAC=\angle ABC = \angle ACB = 60^{\circ}$，$\angle BPC+\angle BAC = 180^{\circ}$（圆内接四边形对角互补），则$\angle BPC = 120^{\circ}$。
所以$\angle CPE=60^{\circ}$，又因为$PE = PC$，所以$\triangle PCE$是等边三角形（有一个角是$60^{\circ}$的等腰三角形是等边三角形）。
则$CE = PC$，$\angle PCE = 60^{\circ}$。
因为$\angle ACB=\angle PCE = 60^{\circ}$，所以$\angle ACB+\angle BCP=\angle PCE+\angle BCP$，即$\angle ACP=\angle BCE$。
在$\triangle ACP$和$\triangle BCE$中，$\left\{\begin{array}{l}AC = BC\\\angle ACP=\angle BCE\\PC = CE\end{array}\right.$，所以$\triangle ACP\cong\triangle BCE(SAS)$。
所以$PA = BE$，又因为$BE = PB + PE$，$PE = PC$，所以$PA = PB + PC$。
$(2)$ 证明$PA = PC+\sqrt{2}PB$
解：过点$B$作$BM\perp PB$交$PA$于$M$。
因为四边形$ABCD$是正方形，所以$\angle BAC = 45^{\circ}$，$\angle ABC = 90^{\circ}$，$\angle BPC+\angle BAC= 180^{\circ}$（圆内接四边形对角互补），则$\angle BPC = 135^{\circ}$。
因为$BM\perp PB$，所以$\angle PBM = 90^{\circ}$，$\angle ABM=\angle ABC-\angle MBC = 90^{\circ}-\angle MBC$，$\angle PBC=\angle PBM+\angle MBC = 90^{\circ}+\angle MBC$，$\angle BMA+\angle BPC = 180^{\circ}$（圆内接四边形外角等于内对角），所以$\angle BMA = 45^{\circ}$。
则$\triangle PBM$是等腰直角三角形（有一个角是$45^{\circ}$的直角三角形是等腰直角三角形），所以$PM=\sqrt{2}PB$，$BM = PB$。
因为$\angle BAC=\angle BMC = 45^{\circ}$（同弧所对的圆周角相等），$\angle ABM+\angle ABP=\angle PBC+\angle ABP$，即$\angle ABM=\angle PBC$。
在$\triangle ABM$和$\triangle CBP$中，$\left\{\begin{array}{l}\angle BMA=\angle BPC = 135^{\circ}\\BM = BP\\\angle ABM=\angle CBP\end{array}\right.$，所以$\triangle ABM\cong\triangle CBP(ASA)$。
所以$AM = PC$。
因为$PA=AM + PM$，$PM=\sqrt{2}PB$，$AM = PC$，所以$PA = PC+\sqrt{2}PB$。
综上，$(1)$得证$PA = PB + PC$；$(2)$得证$PA = PC+\sqrt{2}PB$。