《2025年启东中学作业本九年级数学上册苏科版徐州专版》

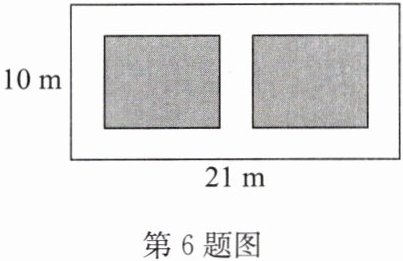
6.如图,有一块长为21m、宽为10m的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间及周边留有宽度相等的人行通道,且人行通道的宽度不能超过3m.
(1)如果两块绿地的面积之和为$90m^2,$求人行通道的宽度;
(2)能否改变人行通道的宽度,使得每块绿地的宽与长之比等于3:5?请说明理由.

答案： 1. （1）
设人行通道的宽度为$x$米$(0\lt x\leqslant3)$。
则每块绿地的长为$\frac{21 - 3x}{2}$米，宽为$(10 - 2x)$米。
根据两块绿地的面积之和为$90m^{2}$，可列方程：
$2×\frac{21 - 3x}{2}×(10 - 2x)=90$。
化简方程：
$(21 - 3x)(10 - 2x)=90$。
展开括号得$210-42x - 30x+6x^{2}=90$。
移项化为一元二次方程的一般形式：$6x^{2}-72x + 120 = 0$，两边同时除以$6$得$x^{2}-12x + 20 = 0$。
分解因式：
根据$x^{2}+(a + b)x+ab=(x + a)(x + b)$，对于$x^{2}-12x + 20 = 0$，其中$a=-2$，$b=-10$，则$(x - 2)(x - 10)=0$。
求解方程：
所以$x - 2 = 0$或$x - 10 = 0$，解得$x_{1}=2$，$x_{2}=10$。
因为$0\lt x\leqslant3$，所以$x = 2$。
2. （2）
设人行通道的宽度为$y$米$(0\lt y\leqslant3)$。
每块绿地的长为$\frac{21 - 3y}{2}$米，宽为$(10 - 2y)$米。
若每块绿地的宽与长之比等于$3:5$，则$\frac{10 - 2y}{\frac{21 - 3y}{2}}=\frac{3}{5}$。
交叉 - 相乘得：
$5(10 - 2y)=3×\frac{21 - 3y}{2}$。
去括号：$50-10y=\frac{63 - 9y}{2}$。
两边同时乘以$2$得：$100 - 20y=63 - 9y$。
移项：$-20y + 9y=63 - 100$。
合并同类项：$-11y=-37$。
解得$y=\frac{37}{11}\approx3.36$。
因为$\frac{37}{11}\gt3$，不满足$0\lt y\leqslant3$。
所以：
(1) 人行通道的宽度为$2m$；
(2) 不能，因为按照宽与长之比为$3:5$计算出的人行通道宽度$y = \frac{37}{11}\gt3$，不满足人行通道宽度不能超过$3m$的条件。

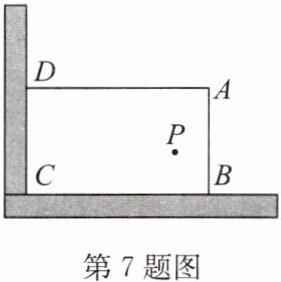
7.(2024·海门市月考)某学校在“美化校园,幸福学习”活动中,计划利用如图所示的直角墙角(阴影部分,两边足够长),用20m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,AD两边).
(1)若花园的面积为$75m^2,$求AB的长;
(2)若在直角墙角内点P处有一棵桂花树,且到墙CD的距离为12m,若要将这棵树围在矩形花园内(含边界,不考虑树的粗细),问该花园的面积能否为$100m^2?$若能,求出AB的长;若不能,请说明理由.

答案：
(1)设AB=x m,则AD=(20-x)m.根据题意,得x(20-x)=75,解得x₁=5,x₂=15.答:AB的长为5 m或15 m.
(2)假设能将这棵树围在矩形花园内,且该花园的面积能为100m².设AD的长为y m.根据题意,得y(20-y)=100,解得y₁=y₂=10.
∵10＜12,
∴要将这棵树围在矩形花园内,该花园的面积不能为100m².

8.(2024·泰兴月考)某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为1:2的矩形(如图),已知栅栏的总长度为24m,设较小矩形的宽为x m.
(1)若矩形养殖场的总面积为$36m^2,$求此时x的值;
(2)该农场想要建一个$50m^2$的矩形养殖场,这一想法能实现吗?请说明理由.

答案：
(1)
∵BC=x m,矩形CDEF的面积是矩形BCFA面积的2倍,
∴CD=2x m,
∴BD=3x m,AB=CF=DE=1/3(24-BD)=(8-x)m.根据题意,得3x(8-x)=36,整理,得x²-8x+12=0,解得x₁=2,x₂=6.当x=2时,3x=3×2=6＜10,符合题意；当x=6时,3x=3×6=18＞10,不符合题意,舍去.答:此时x的值为2.
(2)这一想法不能实现.理由如下:假设这一想法能实现,根据题意,得3x(8-x)=50,整理,得3x²-24x+50=0.
∵b²-4ac=(-24)²-4×3×50=-24＜0,
∴原方程没有实数根,
∴假设不成立,即这一想法不能实现.