《2025年启东中学作业本九年级数学上册苏科版徐州专版》

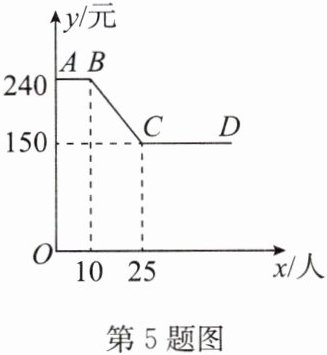
5. 某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图像,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为240元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?

解:设参加这次旅游的人数为 a.
∵10×240=2400＜3600,∴a＞10.
∵25×150=3750＞3600,∴a＜25.
综上可知,10＜a＜25.
设线段 BC 对应的函数表达式为 y=kx+b,
把(10,240),(25,150)代入,得
$\begin{cases}10k+b=240, \\25k+b=150, \end{cases}$解得$\begin{cases}k=-6, \\b=300. \end{cases}$
∴线段 BC 对应的函数表达式为$y=-6x+300(10＜x＜25)$.
∴人数为 a 时的人均收费为(-6a+300)元.
根据题意,得$a(-6a+300)=3600$,
整理,得$a^{2}-50a+600=0$,解得$a_{1}=20$,$a_{2}=30$.
∵10＜a＜25,∴a=20.
答:参加这次旅游的人数为 20.

答案： 5.
(1)240
(2)解:设参加这次旅游的人数为 a.
∵10×240=2400＜3600,
∴a＞10.
∵25×150=3750＞3600,
∴a＜25.
综上可知,10＜a＜25.
设线段 BC 对应的函数表达式为 y=kx+b,
把(10,240),(25,150)代入,得
$\begin{cases}10k+b=240, \\25k+b=150, \end{cases}$解得$\begin{cases}k=-6, \\b=300. \end{cases}$
∴线段 BC 对应的函数表达式为$y=-6x+300(10＜x＜25)$.
∴人数为 a 时的人均收费为(-6a+300)元.
根据题意,得$a(-6a+300)=3600$,
整理,得$a^{2}-50a+600=0$,解得$a_{1}=20$,$a_{2}=30$.
∵10＜a＜25,
∴a=20.
答:参加这次旅游的人数为 20.

6. 某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系: 若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,售出的每部汽车的进价均降低0.1万元. 月底时,厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元;销售量在10部以上,每部返利1万元.
(1)若该公司当月售出3部汽车,则每部汽车的进价为______26.8万元;
(2)如果每部汽车的售价为28万元,该公司计划当月盈利12万元,那么需要售出多少部汽车? (盈利= 销售利润+返利)
解:设需要售出 x 部汽车,由题意可知,每部汽车的销售利润为$28-[27-0.1(x-1)]=(0.1x+0.9)$万元.
当0≤x≤10时,根据题意,得$x(0.1x+0.9)+0.5x=12$,
整理,得$x^{2}+14x-120=0$,
解得$x_{1}=-20$(不合题意,舍去),$x_{2}=6$.
当x＞10时,根据题意,得$x(0.1x+0.9)+x=12$,
整理,得$x^{2}+19x-120=0$,
解这个方程,得$x_{1}=-24$(不合题意,舍去),$x_{2}=5$.
因为5＜10,所以x=5舍去.
答:需要售出 6 部汽车.

答案： 6.
(1)26.8
(2)解:设需要售出 x 部汽车,由题意可知,每部汽车的销售利润为$28-[27-0.1(x-1)]=(0.1x+0.9)$万元.
当0≤x≤10时,根据题意,得$x(0.1x+0.9)+0.5x=12$,
整理,得$x^{2}+14x-120=0$,
解得$x_{1}=-20$(不合题意,舍去),$x_{2}=6$.
当x＞10时,根据题意,得$x(0.1x+0.9)+x=12$,
整理,得$x^{2}+19x-120=0$,
解这个方程,得$x_{1}=-24$(不合题意,舍去),$x_{2}=5$.
因为5＜10,所以x=5舍去.
答:需要售出 6 部汽车.