《2025年小题狂做九年级物理上册苏科版巅峰版》

1. 一辆以汽油为燃料的汽车,以 72 km/h 的速度在水平路面上匀速行驶时,发动机的实际输出功率为 20 kW。若汽车行驶的路程为 108 km,已知汽油的热值 $ q= 4.6× 10^{7}\ \text{J/kg} $。汽车发动机的效率为 25%。则下列说法正确的是(B)
A.行驶的时间为 1 h
B.发动机所做的有用功为 $ 1.08× 10^{8}\ \text{J} $
C.汽车所受的阻力为 2000 N
D.消耗汽油的质量为 5 kg

答案： B 提示:汽车运动的时间$t=\frac{s}{v}=\frac{108\ km}{72\ km/h}=1.5\ h = 5400\ s$;$W_{\text{有用}}=Pt=20× 10^{3}\ W× 5400\ s = 1.08× 10^{8}\ J$;汽车牵引力$F=\frac{P}{v}=\frac{20× 10^{3}\ W}{20\ m/s}=1000\ N$，匀速行驶时，$f = F = 1000\ N$;$Q_{\text{放}}=\frac{W_{\text{有用}}}{\eta}=\frac{1.08× 10^{8}\ J}{25\%}=4.32× 10^{8}\ J$，$m=\frac{Q_{\text{放}}}{q}=\frac{4.32× 10^{8}\ J}{4.6× 10^{7}\ J/kg}\approx 9.4\ kg$。

2. (2024·常州武进模拟)一辆汽车使用的是四冲程内燃机,如图甲是内燃机的一个冲程,该汽车以恒定的功率在水平公路上做直线运动,其速度随时间变化的关系如图乙所示。汽车在行驶过程中所受阻力恒为 4000 N,内燃机的效率为 40%,汽油的热值为 $ 4.6× 10^{7}\ \text{J/kg} $。下列有关叙述正确的是(D)
A. 图甲冲程中内能转化为机械能
B. 汽车一直做匀速直线运动
C. 在 0～20 s 内汽车牵引力所做的功为 $ 8× 10^{5}\ \text{J} $
D. 需要燃烧约 0.043 kg 汽油才能使汽车完成前 10 s 的运动

答案： D 提示:图甲为压缩冲程，将机械能转化为内能;牵引力$F = f = 4000\ N$，$P = Fv = 4000\ N× 20\ m/s = 8× 10^{4}\ W$，0 - 20 s内，$W = Pt = 8× 10^{4}\ W× 20\ s = 1.6× 10^{6}\ J$;$Q_{\text{放}}=\frac{W}{\eta}=\frac{1.6× 10^{6}\ J}{40\%}=4× 10^{6}\ J$，0 - 10 s内，$Q_{\text{放}}'=\frac{1}{2}Q_{\text{放}}=\frac{1}{2}× 4× 10^{6}\ J = 2× 10^{6}\ J$，$m_{\text{汽油}}=\frac{Q_{\text{放}}'}{q}=\frac{2× 10^{6}\ J}{4.6× 10^{7}\ J/kg}\approx 0.043\ kg$。

3. (2024·苏州姑苏模拟)汽油机甲的飞轮每分钟转 2400 转,汽缸容积为 $ 150\ \text{cm}^{3} $,满负荷工作时做功冲程燃气的平均压强为 $ 2.0× 10^{6}\ \text{Pa} $,1 min 消耗 25 g 汽油。汽油机甲与汽油机乙的效率比为 5:4,汽油机甲的功率是乙的 2.5 倍,则汽油机甲的功率和甲、乙汽油机相同时间的油耗之比为(汽油的热值为 $ 4.8× 10^{7}\ \text{J/kg} $)(B)
A.$ 3.6× 10^{6}\ \text{W} $,2:1
B.6000 W,2:1
C.$ 3.6× 10^{6}\ \text{W} $,1:2
D.6000 W,1:2

答案： B 提示:甲一次对外做功$W = FL = pS×\frac{V}{S}=pV = 2.0× 10^{6}\ Pa× 150× 10^{-6}\ m^{3}=300\ J$;1 min甲做功1200次，$W_{\text{甲}} = 1200W = 1200× 300\ J = 3.6× 10^{5}\ J$，$P_{\text{甲}}=\frac{W_{\text{甲}}}{t}=\frac{3.6× 10^{5}\ J}{60\ s}=6000\ W$;1 min内$Q_{\text{甲放}} = m_{\text{甲}}q = 25× 10^{-3}\ kg× 4.8× 10^{7}\ J/kg = 1.2× 10^{6}\ J$，$\eta_{\text{甲}}=\frac{W_{\text{甲}}}{Q_{\text{甲放}}}× 100\%=\frac{3.6× 10^{5}\ J}{1.2× 10^{6}\ J}× 100\% = 30\%$，$\eta_{\text{乙}}=\frac{4}{5}\eta_{\text{甲}} = 24\%$，$P_{\text{乙}}=\frac{P_{\text{甲}}}{2.5}=\frac{6000\ W}{2.5}=2400\ W$，$W_{\text{乙}} = P_{\text{乙}}t = 2400\ W× 60\ s = 1.44× 10^{5}\ J$，$Q_{\text{乙放}}=\frac{W_{\text{乙}}}{\eta_{\text{乙}}}=\frac{1.44× 10^{5}\ J}{24\%}=6× 10^{5}\ J$，$m_{\text{乙}}=\frac{Q_{\text{乙放}}}{q}=\frac{6× 10^{5}\ J}{4.8× 10^{7}\ J/kg}=0.0125\ kg = 12.5\ g$，$m_{\text{甲}}:m_{\text{乙}} = 25\ g:12.5\ g = 2:1$。

4. 某单缸四冲程汽油机的汽缸活塞面积为 $ 30\ \text{cm}^{2} $,1 个冲程活塞在汽缸中移动的距离是 50 mm,满负荷工作时做功冲程燃气的平均压强为 $ 9.0× 10^{5}\ \text{Pa} $,飞轮 1 min 转动 1800 周。当汽油机满负荷工作时(不计摩擦),下列说法正确的是(B)
A.汽油机每秒内完成 30 个冲程
B.汽油机的功率为 2025 W
C.做功冲程中燃气对活塞的平均压力为 $ 2.7× 10^{7}\ \text{N} $
D.一个做功冲程中燃气对活塞做的功为 $ 1.35× 10^{5}\ \text{J} $

答案： B 提示:飞轮1 min转动1800周，每秒转动30周，完成15个工作循环，完成60个冲程;$S = 30\ cm^{2}=3× 10^{-3}\ m^{2}$，燃气对活塞的平均压力$F = pS = 9.0× 10^{5}\ Pa× 3× 10^{-3}\ m^{2}=2700\ N$;$s = 50\ mm = 0.05\ m$，1个做功冲程中燃气对活塞做功$W = Fs = 2700\ N× 0.05\ m = 135\ J$;飞轮1 min对外做功900次，$W_{\text{总}} = W× 900 = 135\ J× 900 = 121500\ J$，汽油机的功率$P=\frac{W_{\text{总}}}{t}=\frac{121500\ J}{60\ s}=2025\ W$。

5. (2024·南通如皋月考)有两台单缸四冲程柴油机,它们在做功冲程中每做功一次,对外输出的有用功相等。甲、乙两柴油机输出的有用功率之比为 4:3,甲柴油机的效率为 32%,乙柴油机的效率为 36%,则甲、乙两柴油机在相同的时间内飞轮的转数之比为______4:3,乙柴油机在某工作时间内消耗了 10 kg 的柴油,则甲柴油机在相等的时间内消耗的柴油为______15kg。

答案： 4:3 15 提示:设甲、乙在$t\ s$内飞轮的转数分别为$n_{\text{甲}}$、$n_{\text{乙}}$，$t\ s$内甲、乙对外做功分别为$\frac{1}{2}n_{\text{甲}}W$和$\frac{1}{2}n_{\text{乙}}W$，$\frac{P_{\text{甲}}}{P_{\text{乙}}}=\frac{\frac{\frac{1}{2}n_{\text{甲}}W}{t}}{\frac{\frac{1}{2}n_{\text{乙}}W}{t}}=\frac{4}{3}$，得$\frac{n_{\text{甲}}}{n_{\text{乙}}}=\frac{4}{3}$;相等时间内甲、乙对外做功之比$\frac{W_{\text{甲}}}{W_{\text{乙}}}=\frac{n_{\text{甲}}}{n_{\text{乙}}}$，因$\eta=\frac{W}{Q}=\frac{W}{mq}$，得$m=\frac{W}{\eta q}$，故$\frac{m_{\text{甲}}}{m_{\text{乙}}}=\frac{\frac{W_{\text{甲}}}{\eta_{\text{甲}} q}}{\frac{W_{\text{乙}}}{\eta_{\text{乙}} q}}=\frac{W_{\text{甲}}\eta_{\text{乙}}}{W_{\text{乙}}\eta_{\text{甲}}}=\frac{n_{\text{甲}}}{n_{\text{乙}}}×\frac{\eta_{\text{乙}}}{\eta_{\text{甲}}}$，$m_{\text{甲}}=\frac{n_{\text{甲}}\eta_{\text{乙}}}{n_{\text{乙}}\eta_{\text{甲}}}× m_{\text{乙}}=\frac{4}{3}×\frac{36\%}{32\%}× 10\ kg = 15\ kg$。

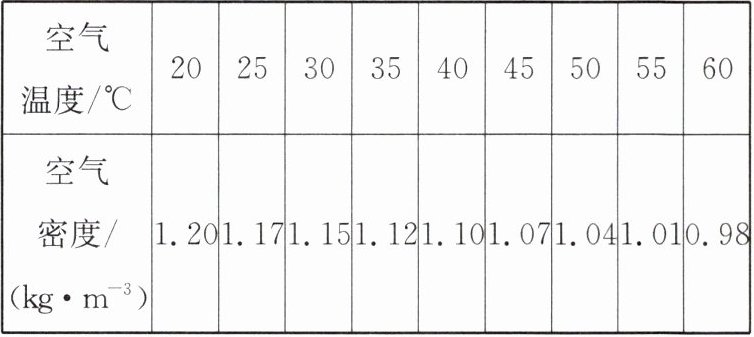
6. (2024·无锡滨湖期中)如图所示,是小明制作的“简易孔明灯”,其体积为 $ 0.2\ \text{m}^{3} $。在孔明灯下端的燃烧皿中加入适量的煤油,将燃烧皿放在电子秤上实时监测其质量的变化。孔明灯的质量为 20 g,室温为 $ 20\ ^{\circ}\text{C} $,当孔明灯刚起飞时,电子秤的示数变化了 1 g,煤油燃烧放出热量$4.6× 10^{4}$J；“孔明灯”刚好起飞时,孔明灯内空气温度约为40$ ^{\circ}\text{C} $；空气吸收的热量最多为4400J；从加热到起飞的过程中,加热效率最大为9.6%(结果保留一位小数)。已知 $ c_{\text{空气}}= 1× 10^{3}\ \text{J/(kg}\cdot^{\circ}\text{C)} $、$ q_{\text{煤油}}= 4.6× 10^{7}\ \text{J/kg} $,g 取 10 N/kg。孔明灯的厚度忽略不计,不同温度下空气密度如表所示。

答案： $4.6× 10^{4}$ 40 4400 9.6 提示:孔明灯刚起飞时，$Q_{\text{放}} = m_{\text{煤油}}q_{\text{煤油}} = 1× 10^{-3}\ kg× 4.6× 10^{7}\ J/kg = 4.6× 10^{4}\ J$，此时有$F_{\text{浮}} = G_{\text{灯}} + G_{\text{气}}$，$\rho_{\text{空气}}gV = m_{\text{灯}}g + \rho_{\text{气}}gV$，即$1.20\ kg/m^{3}× 10\ N/kg× 0.2\ m^{3}=20× 10^{-3}\ kg× 10\ N/kg+\rho_{\text{气}}× 10\ N/kg× 0.2\ m^{3}$，解得$\rho_{\text{气}} = 1.1\ kg/m^{3}$，故灯内空气温度为$40^{\circ}C$，灯内空气吸热$Q_{\text{吸}} = cm(t - t_{0}) = 1× 10^{3}\ J/(kg\cdot^{\circ}C)× 1.1\ kg/m^{3}× 0.2\ m^{3}×(40^{\circ}C - 20^{\circ}C)=4400\ J$，$\eta=\frac{Q_{\text{吸}}}{Q_{\text{放}}}× 100\%=\frac{4400\ J}{4.6× 10^{4}\ J}× 100\%\approx 9.6\%$。