《2025年小题狂做九年级物理上册苏科版巅峰版》

6. (2024·南京联合体模拟)为了比较两种燃料的热值。小明采用如图甲所示的两套完全相同的装置进行实验,烧杯内水的初温和质量相同,实验中忽略热量的损失。

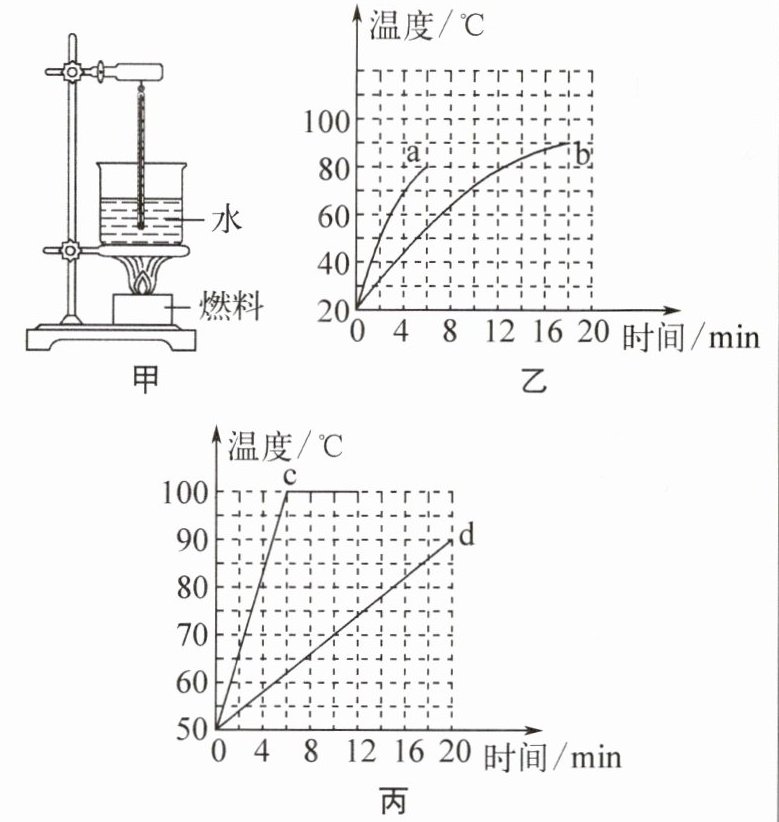
(1)实验中应控制燃料燃烧的______(填“时间”或“质量”)相同,根据______比较燃料燃烧放出热量的多少。
(2)小明选用了燃料a和燃料b进行实验,当燃料燃尽时,小明记下了各个时刻烧杯中的水温,绘制了图乙的图像,则可初步判断燃料______的热值大。
(3)根据图丙得出c、d两种燃料的热值之比为______。

答案： （1）$6.468×10^{6}J$ （2）$4.312×10^{7}J/kg$ （3）17% 提示:（1）$m_{水}=ρ_{水}V_{水}=1×10^{3}kg/m^{3}×0.055m^{3}=55kg,Q_{吸}=c_{水}m_{水}\Delta t=4.2×10^{3}J/(kg\cdot ^{\circ }C)×55kg×(48^{\circ }C-20^{\circ }C)=6.468×10^{6}J$。（2）$Q_{放}=\frac {Q_{吸}}{η}=\frac {6.468×10^{6}J}{75\% }=8.624×10^{6}J,q=\frac {Q_{放}}{m}=\frac {8.624×10^{6}J}{0.2kg}=4.312×10^{7}J/kg$。（3）由$q＜4.6×10^{7}J/kg$可知,该瓶装液化气掺有二甲醚,$m=m_{液化气}+m_{二甲醚}=0.2kg,Q_{放}=m_{液化气}q_{液化气}+m_{二甲醚}q_{二甲醚}=m_{液化气}×4.6×10^{7}J/kg+m_{二甲醚}×2.9×10^{7}J/kg=8.624×10^{6}J$,解得$m_{二甲醚}\approx 0.034kg$,则$\frac {m_{二甲醚}}{m}=\frac {0.034kg}{0.2kg}×100\% =17\% $。

7. (2024·盐城射阳模拟)液化气的热值高达$4.6×10^{7}J/kg$,一些不法商贩为牟取暴利,常将液化气与价格低廉、热值仅为$2.9×10^{7}J/kg$的二甲醚混合装入钢瓶内销售给客户。小李家使用的液化气热水器的铭牌标明的热效率为75%,表示该热水器工作时,液化气完全燃烧所消耗的化学能有多大比例转化成水的内能。为测定家中瓶装液化气是否掺混二甲醚,小李把家里的自动洗衣机的水量设置为55 L,用热水器输出的热水注入洗衣机,当注入水的体积达到55 L时,洗衣机便会自动停止注水,已知当时自来水的温度是$20^{\circ }C$,热水器输出热水的温度是$48^{\circ }C$,这次测定实验共消耗瓶内液化气的质量为0.2 kg。问:
(1)55 L水共吸收多少热量?
(2)该瓶装液化气的热值是多少?
(3)通过计算后说明,该瓶装液化气掺混的二甲醚质量百分比是多少?

答案：
(1)解：水的体积$V=55L=0.055m^{3}$，由$\rho=\frac{m}{V}$得，水的质量$m_{水}=\rho V=1.0×10^{3}kg/m^{3}×0.055m^{3}=55kg$。
水吸收的热量$Q_{吸}=c_{水}m_{水}(t-t_{0})=4.2×10^{3}J/(kg\cdot^{\circ}C)×55kg×(48^{\circ}C - 20^{\circ}C)=4.2×10^{3}×55×28J=6.468×10^{6}J$。
(2)解：由$\eta=\frac{Q_{吸}}{Q_{放}}$得，液化气完全燃烧放出的热量$Q_{放}=\frac{Q_{吸}}{\eta}=\frac{6.468×10^{6}J}{75\%}=8.624×10^{6}J$。
该瓶装液化气的热值$q=\frac{Q_{放}}{m}=\frac{8.624×10^{6}J}{0.2kg}=4.312×10^{7}J/kg$。
(3)解：设0.2kg液化气中液化气的质量为$m_{1}$，二甲醚的质量为$m_{2}$，则$m_{1}+m_{2}=0.2kg$。
$Q_{放}=q_{1}m_{1}+q_{2}m_{2}$，即$8.624×10^{6}J=4.6×10^{7}J/kg× m_{1}+2.9×10^{7}J/kg× m_{2}$。
联立解得$m_{2}=0.048kg$。
二甲醚质量百分比为$\frac{m_{2}}{m}×100\%=\frac{0.048kg}{0.2kg}×100\%=24\%$。
答：
(1)55L水共吸收$6.468×10^{6}J$热量；
(2)该瓶装液化气的热值是$4.312×10^{7}J/kg$；
(3)该瓶装液化气掺混的二甲醚质量百分比是24%。

8. (2024·南京秦淮月考)汽油发动机工作时,汽油必须和吸进的空气成适当的比例,才能形成可以有效燃烧的混合气,这就是空燃比(可燃混合气中空气质量与燃油质量之比)。某总排量为2.0 L的发动机的空燃比为$22:1$,混合燃气的密度为$1.5kg/m^{3}$,则发动机做一次功,燃料燃烧产生的热量为______$6×10^{3}$J,当发动机曲轴每分钟转速为3000转时,此时汽车输出的机械功率为90 kW,此时该发动机的效率是______60%(汽油的热值为$4.6×10^{7}J/kg$)。若该汽油机的效率为20%,年平均消耗汽油420 kg,如果将效率提高了1%,则一年可以节约______20kg的汽油。

答案： $6×10^{3}$ 60 20 提示:$V_{混}=2L=2×10^{-3}m^{3},m_{混}=ρ_{混}V_{混}=1.5kg/m^{3}×2×10^{-3}m^{3}=3×10^{-3}kg,m_{油}=\frac {1}{1+22}m_{混}=\frac {1}{23}×3×10^{-3}kg=\frac {3}{23}×10^{-3}kg,Q_{放}=qm_{油}=4.6×10^{7}J/kg×\frac {3}{23}×10^{-3}kg=6×10^{3}J;3000r/min=50r/s$,1 s 对外做功 25 次,$Q_{放总}=25Q_{放}=25×6×10^{3}J=1.5×10^{5}J,W=Pt=9×10^{4}W×1s=9×10^{4}J,η=\frac {W}{Q_{放总}}×100\% =\frac {9×10^{4}J}{1.5×10^{5}J}×100\% =60\% ;η_{2}=η_{1}+1\% =21\% $,因$W_{有用}$相等,即$η_{1}m_{1}q=η_{2}m_{2}q$,得$m_{2}=\frac {η_{1}m_{1}q}{η_{2}q}=\frac {η_{1}m_{1}}{η_{2}}=\frac {20\% ×420kg}{21\% }=400kg,\Delta m=m_{1}-m_{2}=420kg-400kg=20kg$。