《2025年小题狂做九年级物理上册苏科版巅峰版》

1. (2024·苏州昆山期末)如图所示的甲、乙两个 M 形硬质轻杆可绕中间转轴 O 灵活转动,轻杆两端分别用细绳悬挂两个质量相等的重物,保持平衡状态。用手使两个右端的重物略微下降一小段距离后再松手,能恢复到原来平衡位置的是 ( )
A. 只有甲
B. 只有乙
C. 甲和乙都能
D. 甲和乙都不能

答案：
B　提示:轻杆处于平衡时，悬挂的两重物质量相等，则作用在轻杆两端的拉力相等，如图甲所示，有L₁=L₂，L₃=L₄；将右端重物略微下降一小段距离后，杠杆受力示意图如图乙所示，L₁'＜L₁，L₂'＞L₂，则GL₁'＜GL₂'，故甲杠杆右端的重物继续下降，不能恢复到原平衡位置；L₃'＞L₃，L₄'＜L₄，则GL₃'＞GL₄'，故乙杠杆左端的重物会下降，能恢复到原平衡位置。

2. (2024·南京玄武月考)图甲是跳水运动中的跳板,其可简化为图乙所示的轻质杠杆,A 为支点,跳板左侧 O 点由一竖直轻杆 OB 将跳板固定在水平面上,设人到跳板左端 O 点的距离为 x,O、A 之间的距离为 $x_A$,跳板总长为 L。则下列关于 OB 上弹力大小 F 与 x 的关系图像符合实际的是 (C)

答案： C　提示:当人站在O点时，对OB的弹力等于人的重力；当人向A点移动时，人对杆的压力的力臂减小，因OA间距离xₐ不变，则OB上的弹力F减小；当人站在A点时，对杆的压力的力臂为0，则OB上的弹力F = 0；当人再远离A点时，人对杠杆的压力不变，对杆的压力的力臂增大，则OB上的弹力F增大；A点到右端的距离大于A点到左端的距离，则人在右端时OB受到的弹力大于人的重力。故OB上的弹力F随x的增大，先减小至0，再增大至大于人的重力。

3. 现有一根形变不计、长为 L 的铁条 AB 和两根横截面积相同、长度分别为 $L_a$、$L_b$ 的铝条 a、b,将铝条 a 叠在铁条 AB 上,并使它们的右端对齐,然后把它们放置在三角形支架上,AB 水平平衡,此时 OB 间的距离恰好为 $L_a$,如图所示。取下铝条 a 后,将铝条 b 按上述操作方法使铁条 AB 再次水平平衡,此时 OB 的距离为 $L_x$。下列判断正确的是 ( )


A.若 $L_a ＜ L_b ＜ L$,则 $L_a ＜ L_x ＜ \frac{L_a + L_b}{2}$
B.若 $L_a ＜ L_b ＜ L$,则 $L_x ＞ \frac{L_a + L_b}{2}$
C.若 $L_b ＜ L_a$,则 $\frac{L_a + L_b}{2} ＜ L_x ＜ L_a$
D.若 $L_b ＜ L_a$,则 $L_x ＜ \frac{L_a + L_b}{2}$

答案：
A　提示:若Lₐ＜Lᵦ＜L，用铝条b替换铝条a就相当于在铝条a左侧放了一段长为Lᵦ - Lₐ、重为Gᵦ - Gₐ的铝条，如图甲所示，这一段铝条的重心距B端的长度为Lₐ + (Lᵦ - Lₐ)/2 = (Lₐ + Lᵦ)/2，而铁条AB和铝条a组成的整体的重心在支架原来的位置，距B端的长度为Lₐ，要使铁条AB水平平衡，支架O应移到上述两个重心之间，即Lₐ＜Lₓ＜(Lₐ + Lᵦ)/2。如图乙所示，若Lᵦ＜Lₐ，用铝条b替换铝条a就相当于从铝条a左侧截掉一段长为Lₐ - Lᵦ、重为Gₐ - Gᵦ的铝条，也相当于距B端Lᵦ + (Lₐ - Lᵦ)/2 = (Lₐ + Lᵦ)/2处施加一个竖直向上的力，其大小为Gₐ - Gᵦ，要使铁条AB水平平衡，支架O应向A端移动，则Lₓ＞Lₐ，由Lᵦ＜Lₐ可知Lₓ＞Lₐ=(Lₐ + Lₐ)/2＞(Lₐ + Lᵦ)/2。

4. 如图所示为一轻质硬棒,$AB = BC = CD$,在 A 点悬挂重物 G,C 点在 $F_1$ 作用下使硬棒水平平衡,则硬棒的支点可能是 ______(填“A”“B”“C”或“D”)点。当 $G = 150\ \text{N}$ 时,$F_1$ 的大小为 ______N。若将重物拿走,在 A 点施加一个与 $F_1$ 平行且大小等于 150 N 的力 $F_2$(图中虚线所示),为使硬棒水平平衡,$F_1$ 大小应为 ______N。

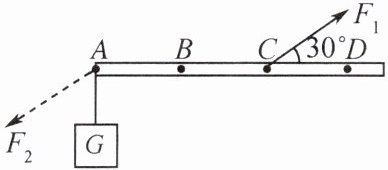
D
900
450

答案： D　900　450　提示:动力与阻力使硬棒的转动方向相反，一个力为顺时针则另一个力为逆时针，故当D为支点时，F₁、G使硬棒转动的方向相反；A、C两点不能为支点，否则无阻力臂或动力臂；B为支点时，F₁、G使硬棒转动的方向相同。因F₁的力臂为CD的一半，即L₁ = 0.5CD，由杠杆平衡条件有G×AD = F₁×0.5CD，得F₁ = G×AD/(0.5CD)=6G = 6×150N = 900N。若将重物拿走，在A点施加一个与F₁平行且大小等于150 N的力F₂，此时F₂的力臂L₂ = 0.5AD，因F₂×0.5AD = F₁'×0.5CD，解得F₁' = F₂×(0.5AD)/(0.5CD)=3×150N = 450N。

5. (2024·南京鼓楼模拟)晓欢同学设计了如图所示的装置探究杠杆的平衡条件,在轻质杠杆 AB 的 A 端悬挂一个质量为 3.0 kg 的空桶,$AO:OB = 3:1$。将质量分布均匀、重为 270 N 的异形工件 M 通过细线与 B 端相连,已知 M 的上下两部分均为正方体,且棱长之比为 1:2。此时,杠杆在水平位置平衡,且 M 对地面的压强为 4500 Pa。不考虑机械的摩擦,则此时细线对 M 的拉力为 ______N。若在 M 的下部沿竖直方向截去部分,并将其放入空桶中,使 M 对地面的压强变为原来的 $\frac{32}{45}$,则截去部分的质量为 ______kg。(g 取 $10\ \text{N/kg}$)

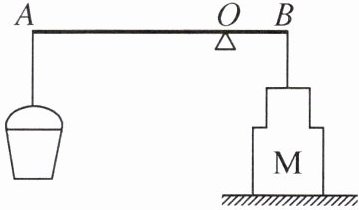
[答案]：90　1.5

答案： 90　1.5　提示:Fₐ = G桶 = m桶g = 3kg×10N/kg = 30N，细线对M的拉力Fᵦ = (OA/OB)×Fₐ = 3×30N = 90N，M对地面的压力F压 = F支 = Gₘ - Fᵦ = 270N - 90N = 180N，M的底面积S = F压/p = 180N/4500Pa = 0.04m²，则M下半部分的棱长为0.2m，上半部分的棱长为0.1m，Vₘ = (0.2m)³ + (0.1m)³ = 9×10⁻³m³，mₘ = Gₘ/g = 270N/10N/kg = 27kg，ρₘ = mₘ/Vₘ = 27kg/(9×10⁻³m³)=3×10³kg/m³；设切去部分的质量为m，切去部分的底面积S切 = m/(ρₘa下)，M与地面的接触面积S' = S - S切 = S - m/(ρₘa下)，p' = (32/45)p = (32/45)×4500Pa = 3200Pa，F'支 = F'压 = p'S' = p'(S - m/(ρₘa下))，F'ᵦ = (Gₘ - mg) - F'支，F'ᵦ = (OA/OB)×(G桶 + mg)=3(G桶 + mg)，解得m = (Gₘ - 3G桶 - p'S')/(4g - p'/(ρₘa下))=(270N - 3×30N - 3200Pa×0.04m²)/(4×10N/kg - 3200Pa/(3×10³kg/m³×0.2m))≈1.5kg。