第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
6. (2024·泸州中考)如图所示,忽略绳重及绳与滑轮间的摩擦,将物体放在水平粗糙桌面上,受到水平向左的恒力$F= 100\ \text{N}$。滑轮组绳子自由端受到的拉力$F_{\text{绳}}为60\ \text{N}$时,物体处于静止状态,物体与桌面间的摩擦力恰好为$0$,则动滑轮的重力为______

20
$\text{N}$;当绳子自由端拉力$F_{\text{绳}}为90\ \text{N}$时,物体水平向右匀速运动,物体与桌面之间的滑动摩擦力为______60
$\text{N}$;撤去水平向左的恒力$F$,改变绳子自由端拉力$F_{\text{绳}}$的大小,仍使物体水平向右做匀速运动时,滑轮组的机械效率为______75%
。
答案:
20 60 75% 提示:当物体静止时,且物体与桌面间的摩擦力为0,不计绳重及绳与滑轮间的摩擦,$F_{绳}=\frac {1}{2}(F+G_{动})$,$G_{动}=2F_{绳}-F=2×60N-100N=20N$;当物体向右匀速运动时,滑轮组受到的拉力$F_{拉}=F+f$,$F'_{绳}=\frac {1}{2}(F_{拉}+G_{动})=\frac {1}{2}(F+f+G_{动})$,$f=2F'_{绳}-F-G_{动}=2×90N-100N-20N=60N$;当撤去F,仍使物体向右匀速运动时,$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {W_{有用}}{W_{有用}+W_{额外}}×100\% =\frac {fs_{物}}{fs_{物}+G_{动}s_{物}}×100\% =\frac {f}{f+G_{动}}×100\% =\frac {60N}{60N+20N}×100\% =75\% $。
7. 如图所示,在相同时间内将重物从梯形平台底端拉至顶端,已知物重为$10\ \text{N}$,$F_{1}= 20\ \text{N}$,$F_{2}= 15\ \text{N}$,平台高度$h= 1\ \text{m}$,斜面长$L_{BA}= 2\ \text{m}$,$L_{CD}= 3\ \text{m}$,则两次过程拉力做功的功率$P_{1}$
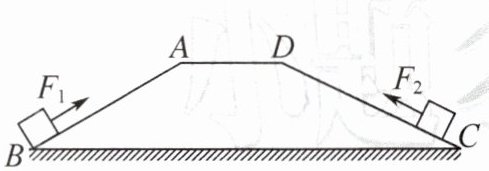
<
(填“$>$”“$=$”或“$<$”,下同)$P_{2}$,机械效率$\eta_{1}$>
$\eta_{2}$,物体沿斜面$AB$运动过程中所受摩擦力大小为15
$\text{N}$。
答案:
< > 15 提示:$W_{总1}=F_{1}L_{BA}=20N×2m=40J$,$W_{总2}=F_{2}L_{CD}=15N×3m=45J$,故$W_{总1}<W_{总2}$,拉力做功的时间相同,则$P_{1}<P_{2}$;都将同一物体提升相同高度,$W_{有用}=Gh=10N×1m=10J$,第一次的总功较小,机械效率较大,则$η_{1}>η_{2}$;$W_{额外}=W_{总1}-W_{有用}=40J-10J=30J$,物体沿斜面AB运动时,$f=\frac {W_{额外}}{L_{BA}}=\frac {30J}{2m}=15N$。
8. 用五个相同的滑轮和绳子组成如图所示的甲、乙两个滑轮组,分别将不同的物体$G_{1}和G_{2}$匀速提升相同高度,绳端所需的拉力$F$恰好相等,不计摩擦、绳和木板的重。则绳端拉力$F做的功之比W_{1}:W_{2}= $
$1:2$
,滑轮组的机械效率之比$\eta_{1}:\eta_{2}= $$1:1$
。
答案:
$1:2$ $1:1$ 提示:图中$n_{甲}=2$,$n_{乙}=4$,$G_{1}$和$G_{2}$匀速提升相同高度,绳端所需的拉力F相等,$s_{1}=2h$,$s_{2}=4h$,绳端拉力F做功之比$\frac {W_{1}}{W_{2}}=\frac {Fs_{1}}{Fs_{2}}=\frac {s_{1}}{s_{2}}=\frac {2h}{4h}=\frac {1}{2}$;由$F=\frac {1}{n}(G_{动}+G)$得$G_{1}=2F-G_{动}$,$G_{2}=4F-2G_{动}$,因$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {Gh}{Fs}×100\% =\frac {G}{nF}×100\% $,故$\frac {η_{1}}{η_{2}}=\frac {G_{1}}{2F}:\frac {G_{2}}{4F}=\frac {2F-G_{动}}{2F}:\frac {4F-2G_{动}}{4F}=\frac {2F-G_{动}}{2F}:\frac {2×(2F-G_{动})}{2×2F}=1:1$。
9. 如图所示,质量分布均匀的长方体薄砖,$ab\lt bc$,平放在水平地面上。图甲用竖直向上的力$F_{1}作用于ab$的中点,图乙用竖直向上的力$F_{2}作用于bc$的中点,都使它们在竖直方向上慢慢向上移动,砖的着地端没有离开地面,两次都使砖的重心升高了$h$,此时两块薄砖都变成了斜面,则:
 (1)在上述过程中,$F_{1}$______
(1)在上述过程中,$F_{1}$______
(2)$F_{1}$所做的功______
(3)若将同一小车分别沿甲、乙两个薄砖斜面的底端匀速拉到顶端,两次机械效率$\eta_{1}$______
 (1)在上述过程中,$F_{1}$______
(1)在上述过程中,$F_{1}$______=
(填“$<$”“$>$”或“$=$”)$F_{2}$。(2)$F_{1}$所做的功______
等于
$F_{2}$所做的功,第一次克服重力所做的功______等于
第二次克服重力所做的功。(均填“大于”“小于”或“等于”)(3)若将同一小车分别沿甲、乙两个薄砖斜面的底端匀速拉到顶端,两次机械效率$\eta_{1}$______
<
(填“$>$”“$<$”或“$=$”)$\eta_{2}$。
答案:
(1)=
(2)等于 等于
(3)< 提示:
(1)图甲中以与地面接触的边cd为支点转动,$F_{1}$克服重力做功才能将砖抬起,即$F_{1}×cb=mg×\frac {cb}{2}$,$F_{1}=\frac {mg}{2}$;同理,图乙中有$F_{2}×ab=mg×\frac {ab}{2}$,$F_{2}=\frac {mg}{2}$,故$F_{1}=F_{2}$。
(2)两次都使重心升高了h,拉力所做的功即克服物体重力所做的功,由$W=Gh$知克服重力做功相同,拉力做功也相同。
(3)砖的重心上升的高度是相同的,则甲与水平面的倾角要小于乙与水平面的倾角;若将同一小车分别沿甲、乙两个薄砖斜面的底端匀速拉到顶端,倾角越小,机械效率越小,故甲的机械效率小于乙的机械效率,即$η_{1}<η_{2}$。
(1)=
(2)等于 等于
(3)< 提示:
(1)图甲中以与地面接触的边cd为支点转动,$F_{1}$克服重力做功才能将砖抬起,即$F_{1}×cb=mg×\frac {cb}{2}$,$F_{1}=\frac {mg}{2}$;同理,图乙中有$F_{2}×ab=mg×\frac {ab}{2}$,$F_{2}=\frac {mg}{2}$,故$F_{1}=F_{2}$。
(2)两次都使重心升高了h,拉力所做的功即克服物体重力所做的功,由$W=Gh$知克服重力做功相同,拉力做功也相同。
(3)砖的重心上升的高度是相同的,则甲与水平面的倾角要小于乙与水平面的倾角;若将同一小车分别沿甲、乙两个薄砖斜面的底端匀速拉到顶端,倾角越小,机械效率越小,故甲的机械效率小于乙的机械效率,即$η_{1}<η_{2}$。
10. 小明在探究“斜面的机械效率”实验中,用长度$s= 0.50\ \text{m}$的木板搭成一个斜面,用弹簧测力计将重为$G= 5.0\ \text{N}$的物块从斜面底端匀速拉至斜面顶端。
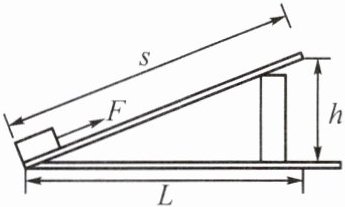
(1)小明在实验中,调整斜面的高度$h= 0.22\ \text{m}$,将物块从斜面底端匀速拉至顶端的过程中,弹簧测力计的示数$F= 4.0\ \text{N}$,则有用功为______$\text{J}$,机械效率为______。
(2)小明利用上述器材进一步研究发现,木板搭成倾角不同的斜面时,将物块从斜面底端匀速拉至斜面顶端的过程中,$W_{\text{额外}}与斜面的水平长度L$(木板在水平面上的正投影长度)有如下关系:
|$L/\text{m}$|$0.45$|$0.40$|$0.35$|$0.30$|
|$W_{\text{额外}}/\text{J}$|$0.90$|$0.80$|$0.70$|$0.60$|
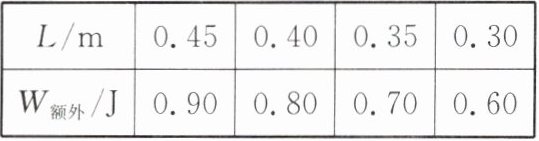
通过数据分析,小明得出初步结论:$W_{\text{额外}}与L$成______比,小明查阅资料后证实此结论是正确的。根据此结论,当斜面的水平长度$L= 0.40\ \text{m}$时,斜面的机械效率为______;当木板平放在水平桌面上,水平匀速拉动木板上的物块时,弹簧测力计的示数为______$\text{N}$。
[答案]:(1)
(2)

(1)小明在实验中,调整斜面的高度$h= 0.22\ \text{m}$,将物块从斜面底端匀速拉至顶端的过程中,弹簧测力计的示数$F= 4.0\ \text{N}$,则有用功为______$\text{J}$,机械效率为______。
(2)小明利用上述器材进一步研究发现,木板搭成倾角不同的斜面时,将物块从斜面底端匀速拉至斜面顶端的过程中,$W_{\text{额外}}与斜面的水平长度L$(木板在水平面上的正投影长度)有如下关系:
|$L/\text{m}$|$0.45$|$0.40$|$0.35$|$0.30$|
|$W_{\text{额外}}/\text{J}$|$0.90$|$0.80$|$0.70$|$0.60$|

通过数据分析,小明得出初步结论:$W_{\text{额外}}与L$成______比,小明查阅资料后证实此结论是正确的。根据此结论,当斜面的水平长度$L= 0.40\ \text{m}$时,斜面的机械效率为______;当木板平放在水平桌面上,水平匀速拉动木板上的物块时,弹簧测力计的示数为______$\text{N}$。
[答案]:(1)
1.1
55%
(2)
正
65.2%
2
答案:
(1)1.1 55%
(2)正 65.2% 2 提示:
(1)$W_{有用}=Gh=5N×0.22m=1.1J$,$W_{总}=Fs=4N×0.5m=2J$,斜面的机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {1.1J}{2J}×100\% =55\% $。
(2)由表中数据知,$W_{额外}$与L成正比;当斜面的水平长度$L=0.40m$时,斜面高度$h'=\sqrt {s^{2}-L^{2}}=\sqrt {(0.5m)^{2}-(0.4m)^{2}}=0.3m$,$W'_{有用}=Gh'=5N×0.3m=1.5J$,$W'_{总}=W'_{有用}+W_{额外}=1.5J+0.80J=2.3J$,$η'=\frac {W'_{有用}}{W'_{总}}×100\% =\frac {1.5J}{2.3J}×100\% \approx 65.2\% $;木板平放时,斜面的水平长度$L=s=0.50m$,$\frac {0.45m}{0.90J}=\frac {0.50m}{W'_{额外}}$,$W'_{额外}=1J$,$f=\frac {W'_{额外}}{s}=\frac {1J}{0.50m}=2N$,物体做匀速运动,弹簧测力计的拉力$F=f=2N$。
(1)1.1 55%
(2)正 65.2% 2 提示:
(1)$W_{有用}=Gh=5N×0.22m=1.1J$,$W_{总}=Fs=4N×0.5m=2J$,斜面的机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {1.1J}{2J}×100\% =55\% $。
(2)由表中数据知,$W_{额外}$与L成正比;当斜面的水平长度$L=0.40m$时,斜面高度$h'=\sqrt {s^{2}-L^{2}}=\sqrt {(0.5m)^{2}-(0.4m)^{2}}=0.3m$,$W'_{有用}=Gh'=5N×0.3m=1.5J$,$W'_{总}=W'_{有用}+W_{额外}=1.5J+0.80J=2.3J$,$η'=\frac {W'_{有用}}{W'_{总}}×100\% =\frac {1.5J}{2.3J}×100\% \approx 65.2\% $;木板平放时,斜面的水平长度$L=s=0.50m$,$\frac {0.45m}{0.90J}=\frac {0.50m}{W'_{额外}}$,$W'_{额外}=1J$,$f=\frac {W'_{额外}}{s}=\frac {1J}{0.50m}=2N$,物体做匀速运动,弹簧测力计的拉力$F=f=2N$。
查看更多完整答案,请扫码查看


