《2025年小题狂做九年级物理上册苏科版巅峰版》

10. (2024·苏州虎丘月考)航模飞机(图甲)的表演极具观赏性。这种航模飞机需在跑道上加速滑行一段距离,获得足够的升力后才能起飞。已知航模飞机在起飞离地前,平直跑道对它的支持力$F_{支}$与滑行距离s的关系如图乙所示。发动机产生的推力为300 N,滑行中获得的升力为$F_{升}= cv^{2}$,式中比例系数$c= 7.5N·s^{2}/m^{2}$,v是航模飞机的滑行速度。g取10 N/kg,根据图像解答下列问题:
(1)航模飞机的质量为108kg,起飞过程中发动机做的功为9000J。
(2)航模飞机起飞离地时获得的速度为12m/s。
(3)根据航模飞机在竖直方向的受力和图乙的解析式,推导其滑行距离s与滑行速度v之间的关系式:$s=\dfrac{5}{24}v^{2}\ \text{m}$。

答案：
(1) $108$ $9\ 000$
(2) $12$
(3) $s=\dfrac{5}{24}v^{2}\ \text{m}$ 提示:
(1) 飞机静止时,$G=F_{\text{支}0}=1\ 080\ \text{N}$,$m=\dfrac{G}{g}=\dfrac{1\ 080\ \text{N}}{10\ \text{N/kg}}=108\ \text{kg}$;飞机起飞前滑行的距离$s=30\ \text{m}$,$W=Fs=300\ \text{N} × 30\ \text{m}=9\ 000\ \text{J}$。
(2) 飞机刚离地时,$F_{\text{升}}=G=1\ 080\ \text{N}$,$v=\sqrt{\dfrac{F_{\text{升}}}{c}}=\sqrt{\dfrac{1\ 080\ \text{N}}{7.5\ \text{N} \cdot \text{s}^{2}/\text{m}^{2}}}=12\ \text{m/s}$。
(3) 设$F_{\text{支}}=ks+b$,$s_{1}=0$时,$F_{\text{支}}=1\ 080\ \text{N}$,$s_{2}=30\ \text{m}$时,$F_{\text{支}}=0$,得$F_{\text{支}}=-36s\ \text{N}+1\ 080\ \text{N}$;滑行过程中,$G=F_{\text{升}}+F_{\text{支}}$,即$1\ 080\ \text{N}=cv^{2}\ \text{N}+(1\ 080-36s)\ \text{N}$,解得$s=\dfrac{5}{24}v^{2}\ \text{m}$。

11. 动车组是由至少两节机车或带动力的车厢(动力车)和若干节不带动力的车厢(拖车)所组成的列车。假设每节车厢的总质量均为$7.5×10^{4}kg$,其中第一节和最后一节带动力,它们的额定功率分别为$3.6×10^{7}W和2.4×10^{7}W$,车在行驶过程中阻力恒为重力的0.1倍。(g取10 N/kg)
(1)有一动车组共由8节车厢连接而成,30 min内沿平直轨道匀速行驶了90 km,求动力车牵引力做的功和它的实际功率。
5.4 × 10^{10} J3 × 10^{7} W
(2)若动车组只开动了某一节的动力,动车组行驶时的速度v与它所受的牵引力F之间的关系如图所示(即保持额定功率不变),则这列动车组动力来自第一节(填“第一节”或“最后一节”)车厢。
(3)若动车组以恒定的功率$6×10^{7}W$(同时开动第一、最后一节的动力)沿平直轨道行驶,如果限定动车组的速度不超过80 m/s,那么动车组至少由几节车厢组成?
10

答案：
(1) $5.4 × 10^{10}\ \text{J}$ $3 × 10^{7}\ \text{W}$
(2) 第一节
(3) $10$ 提示:
(1) 动车匀速行驶,$F=f=kmmg=0.1 × 8 × 7.5 × 10^{4}\ \text{kg} × 10\ \text{N/kg}=6 × 10^{5}\ \text{N}$,$W=Fs=6 × 10^{5}\ \text{N} × 90\ 000\ \text{m}=5.4 × 10^{10}\ \text{J}$,$t=30\ \text{min}=1\ 800\ \text{s}$,$P=\dfrac{W}{t}=\dfrac{5.4 × 10^{10}\ \text{J}}{1\ 800\ \text{s}}=3 × 10^{7}\ \text{W}$。
(2) 图中横、纵坐标的乘积表示功率,$P=Fv=1\ 800 × 10^{3}\ \text{N} × 20\ \text{m/s}=3.6 × 10^{7}\ \text{W}$,故动车组动力来自第一节车厢。
(3) 牵引力$F'=\dfrac{P}{v}=\dfrac{6 × 10^{7}\ \text{W}}{80\ \text{m/s}}=7.5 × 10^{5}\ \text{N}$,动车组匀速行驶,$F'=f'=kn'mg$,解得$n'=10$。

12. 学校机器人兴趣小组进行“精准吊装”实验,7块长短不一的长方体木块均平放在水平地面上,机器人将木块按长度从大到小依次吊装并对称叠放。已知木块的密度相同,高度均为$h= 0.2m$,宽度均为$b= 0.2m$,不同序号木块的质量如下表,其中$m= 12kg$,g取10 N/kg。

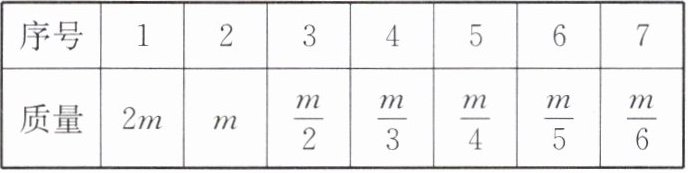
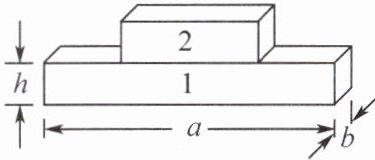
(1)已知1号木块的长度$a= 1.2m$,求未叠放时1号木块对地面的压强。
(2)如图所示,把2号木块吊装到1号木块的上面,求此过程中克服重力所做的功。
(3)机器人完成全部吊装叠放用时6 min,求整个过程克服木块重力做功的功率。

答案：
(1) $1\ 000\ \text{Pa}$
(2) $24\ \text{J}$
(3) $0.4\ \text{W}$ 提示:
(1) 1号木块对地面的压力$F_{1}=G_{1}=m_{1}g=2mg=2 × 12\ \text{kg} × 10\ \text{N/kg}=240\ \text{N}$,未叠放时,1号木块对地面的压强$p_{1}=\dfrac{F_{1}}{S_{1}}=\dfrac{240\ \text{N}}{0.24\ \text{m}^{2}}=1\ 000\ \text{Pa}$。
(2) 克服木块重力所做的功$W=G_{2}h=m_{2}gh=mgh=12\ \text{kg} × 10\ \text{N/kg} × 0.2\ \text{m}=24\ \text{J}$。
(3) 吊装$k$号木块克服重力做功$W_{k}=G_{k}(k-1)h=\dfrac{mg}{(k-1)}(k-1)h=mgh=24\ \text{J}$,吊装每一块木块克服重力做的功相等,$W=6W_{k}=6 × 24\ \text{J}=144\ \text{J}$,克服木块重力做功的功率$P=\dfrac{W}{t}=\dfrac{144\ \text{N}}{360\ \text{s}}=0.4\ \text{W}$。