《2025年小题狂做九年级物理上册苏科版巅峰版》

6. 小熊在课外实践活动中,用如图甲所示的滑轮组匀速拉动放在水平面上的不同物体,物体受到的摩擦力从100 N开始逐渐增加,每次物体被拉动的距离均为1 m。根据测量结果画出了该滑轮组机械效率与物体受到的摩擦力大小的关系图像,如图乙所示,则动滑轮重为100N。若不计绳重和绳与滑轮间的摩擦,当滑轮组的机械效率为75%,物体以0.1 m/s的速度匀速运动时,该滑轮组的有用功的功率是30W。

答案： 100 30 提示:当$f_{1}=100N$时,$η_{1}=50\%,W_{有1}=f_{1}s$,不计绳重及绳与滑轮间的摩擦,$W_{额外}=G_{动}s,W_{总1}=f_{1}s+G_{动}s,η_{1}=\frac {W_{有1}}{W_{总1}}×100\% =\frac {f_{1}s}{f_{1}s+G_{动}s}×100\% =\frac {f_{1}}{f_{1}+G_{动}}×100\% =\frac {100N}{100N+G_{动}}×100\% =50\% $,解得$G_{动}=100N$;当$η_{2}=75\% $时,$η_{2}=\frac {W_{有2}}{W_{总2}}×100\% =\frac {f_{2}s}{f_{2}s+G_{动}s}×100\% =\frac {f_{2}}{f_{2}+G_{动}}×100\% =\frac {f_{2}}{f_{2}+100N}×100\% =75\% $,解得$f_{2}=300N,P_{有}=\frac {W_{有2}}{t}=\frac {f_{2}s}{t}=f_{2}v=300N×0.1m/s=30W$。

7. (2024·泰州姜堰月考)如图所示,两个正方体A、B的重力之比Gₐ:Gᵦ= 3:4。用两组滑轮组分别匀速提升A、B两物体,拉力分别为$F_1、$$F_2,$机械效率分别为$η_1、$$η_2,$两动滑轮重均为G动,忽略绳重和摩擦$,F_1= 120 N,η_1＞50%,η_2-η_1= 5%,$则$F_2=$225N。

答案： 225 提示:不计绳重和摩擦时,$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {W_{有用}}{W_{有用}+W_{额外}}×100\% =\frac {G}{G+G_{动}}×100\% ,η_{1}=\frac {G_{A}}{G_{A}+G_{动}}×100\% =\frac {\frac {3}{4}G_{B}}{\frac {3}{4}G_{B}+G_{动}}×100\% =\frac {3G_{B}}{3G_{B}+4G_{动}}×100\% ,η_{2}=\frac {G_{B}}{G_{B}+G_{动}}×100\% $,则$η_{2}-η_{1}=\frac {G_{B}}{G_{B}+G_{动}}-\frac {3G_{B}}{3G_{B}+4G_{动}}=5\% $,解得$G_{B1}=\frac {1}{3}G_{动},G_{B2}=4G_{动}$,由$η_{1}=\frac {3G_{B}}{3G_{B}+4G_{动}}＞50\% $,解得$G_{B}＞\frac {4}{3}G_{动}$,故$G_{B}=4G_{动},G_{A}=\frac {3}{4}G_{B}=\frac {3}{4}×4G_{动}=3G_{动},F_{1}=\frac {1}{3}(G_{A}+G_{动})=\frac {1}{3}(3G_{动}+G_{动})=\frac {4}{3}G_{动},G_{动}=\frac {3}{4}F_{1}=\frac {3}{4}×120N=90N,G_{B}=4G_{动}=4×90N=360N,F_{2}=\frac {1}{2}(G_{B}+G_{动})=\frac {1}{2}×(360N+90N)=225N$。

8. 体重为700 N的小明站在地面上,用如图所示的滑轮组提起物体A,当物体A匀速竖直上升时,小明对地面的压强为$p_1,$滑轮组的机械效率为$η_1；$在物体A的下方再加挂一个质量为60 kg的物体B后(图中未画出),小明继续通过绳子使物体A和B一起匀速竖直上升,此时他对地面的压强为$p_2,$滑轮组的机械效率为$η_2。$若滑轮组的摩擦及绳重均可忽略不计,且$p_1:p_2= 3:1,η_1:η_2= 9:10,$则滑轮组的机械效率$η_1=$75%。(g取10 N/kg)

答案： 75 提示:由图可知,$n=3$,则$F_{1}=\frac {G_{A}+G_{动}}{3},η_{1}=\frac {G_{A}}{G_{A}+G_{动}}×100\% ,p_{1}=\frac {G-F_{1}}{S}$;同理,再加上物体B后,$F_{2}=\frac {G_{A}+G_{动}+G_{B}}{3},η_{2}=\frac {G_{A}+G_{B}}{G_{A}+G_{动}+G_{B}}×100\% ,p_{2}=\frac {G-F_{2}}{S}$。根据$p_{1}:p_{2}=3:1$,可得$F_{1}=3F_{2}-1400N,G_{A}+G_{动}=1200N$,则$F_{1}=400N,F_{2}=600 N$。根据$η_{1}:η_{2}=9:10$,可得$G_{A}=900N$,则$η_{1}=\frac {G_{A}}{G_{A}+G_{动}}×100\% =\frac {900N}{1200N}×100\% =75\% $。

9. (2024·南通启东期中)甲、乙、丙三人用如图所示的装置提起重物。端点为A、B的木棒中点为C,端点为D、H的木棒中点为E。两根木棒质地均匀,均为圆柱体,重力均为100 N,重物的重力为1800 N。A、B、H是三人对木棒施力的作用点,C与D之间、E与重物之间均通过轻绳相连。三人用竖直向上的力使两根木棒始终以相同的速度同步匀速提升重物(不计轻绳的质量及空气的阻力,g取10 N/kg)。则：

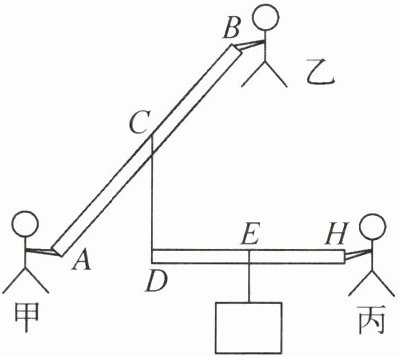
(1)提起重物的过程中,轻绳对D点的拉力Fᴅ=950N。
(2)将重物提升的高度为1 m,整个装置在此过程中的机械效率η=90%。
(3)若用该装置同步匀速提升另一重物M,三个人所用的力刚好相等,则M的质量m=10kg。

答案：
(1) 950
(2) 90%
(3) 10 提示:
(1)以H为支点时,$F_{D}×DH=(G_{物}+G_{棒})×EH$,解得$F_{D}=\frac {EH}{DH}×(G_{物}+G_{棒})=\frac {1}{2}×(1800N+100N)=950N$。
(2)$W_{有用}=G_{物}h=1800N×1m=1800J,W_{额外}=2×G_{棒}h=2×100N×1m=200J,W_{总}=W_{额外}+W_{有用}=200J+1800J=2000J,η=\frac {W_{有用}}{W_{总}}×100\% =\frac {1800J}{2000J}×100\% =90\% $。
(3)若三人施力皆为F,AB棒平衡时,$2F=F'_{D}+G_{棒}$,DH棒平衡时,$G_{棒}+mg=F'_{D}+F,F'_{D}=\frac {1}{2}(G_{棒}+mg)$,解得$F=G_{棒}=100N,mg=2F-G_{棒}=100N,m=\frac {100N}{10N/kg}=10kg$。

10. 小明用如图所示的装置探究杠杆的机械效率,每个钩码的质量为m,O为支点。

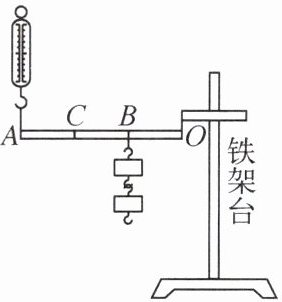
(1)他将2只钩码悬挂在B点,在A点竖直向上匀速拉动弹簧测力计,拉力为$F_1,$测得A、B两点上升的高度分别为$h_1、$$h_2,$则此次杠杆的机械效率为η=$\frac {2mgh_{2}}{F_{1}h_{1}}×100\% $(用物理量的符号表示)。
(2)他将2只钩码悬挂在C点,在A点竖直向上匀速拉动弹簧测力计,使C点上升高度为$h_2,$则弹簧测力计的示数将大于(填“大于”“等于”或“小于”,下同$)F_1,$此次弹簧测力计做的功将小于第一次做的功。
(3)他将3只钩码悬挂在C点,在A点竖直向上匀速拉动弹簧测力计,使C点上升高度仍为$h_2,$则第三次杠杆的机械效率与前两次相比最大(填“最大”“最小”或“三次相等”)。

答案：
(1)$\frac {2mgh_{2}}{F_{1}h_{1}}×100\% $
(2)大于 小于
(3)最大 提示:
(1)有用功$W_{有用}=Gh_{2}=2mgh_{2}$,总功$W_{总}=F_{1}h_{1}$,则机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {2mgh_{2}}{F_{1}h_{1}}×100\% $。
(2)钩码悬挂点由B点移到C点时,阻力臂变大,弹簧测力计的示数变大;钩码重不变,使C点上升高度为$h_{2}$,与使B点上升高度为$h_{2}$相比,有用功不变,但杠杆提升的高度减小,由$W_{额外}=G_{杠杆}h_{杠杆}$知,额外功减小;又因为总功等于额外功与有用功之和,此次弹簧测力计做的功(即总功)将小于第一次做的功。
(3)因为第一次与第二次的有用功相等,且第二次的额外功小,故第一次的机械效率小于第二次的机械效率;将3只钩码悬挂在C点时,物体升高的高度不变,物重增加,有用功变大,但杠杆提升的高度与第二次相同,额外功与第二次相同,故第三次的机械效率大于第二次的机械效率。